Предмет: Алгебра,
автор: nine2009
Помогите,пожалуйста,решить неравенство!
log2|3x/(4x-3)|<=0
Приложения:
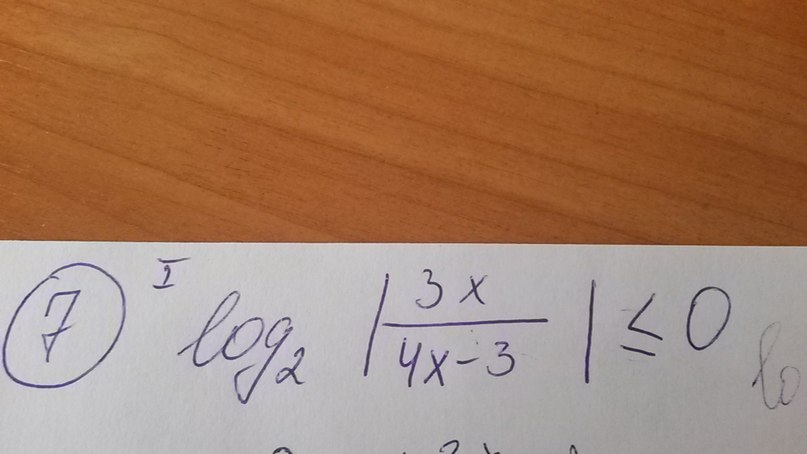
Ответы
Автор ответа:
0
ОДЗ
1) знаменатель не должен обращаться в нуль
4x-3≠0
x≠3/4
2) выражение под логарифмом должно быть положительно, т.к модуль всегда не отрицательный, значит нужно исключить случай равенства нулю числителя
3x≠0
x≠0
Значит x∈(-беск, 0)U(0,3/4)U(3/4, +беск)

т.к 2>1 (основание логарифма), значит просто переходим к выражению стоящему под знаком логарифма без измерения знака неравенства


1) пусть x∈(-беск, 0), тогда оба выражения под модулями отрицательно, значит меняем знак при раскрытии модуля

с учетом условия 1), получаем что x<0
2) пусть x∈(0,3/4), выражение в модуле числителя положительно, в знаменателе - отрицаткльно

значит х∈(0,3/7)
3) x∈(3/4, +беск)

значит x∈[3,+беск)
ОТВЕТ
x∈(-беск, 0)U(3/4,+беск)
1) знаменатель не должен обращаться в нуль
4x-3≠0
x≠3/4
2) выражение под логарифмом должно быть положительно, т.к модуль всегда не отрицательный, значит нужно исключить случай равенства нулю числителя
3x≠0
x≠0
Значит x∈(-беск, 0)U(0,3/4)U(3/4, +беск)
т.к 2>1 (основание логарифма), значит просто переходим к выражению стоящему под знаком логарифма без измерения знака неравенства
1) пусть x∈(-беск, 0), тогда оба выражения под модулями отрицательно, значит меняем знак при раскрытии модуля
с учетом условия 1), получаем что x<0
2) пусть x∈(0,3/4), выражение в модуле числителя положительно, в знаменателе - отрицаткльно
значит х∈(0,3/7)
3) x∈(3/4, +беск)
значит x∈[3,+беск)
ОТВЕТ
x∈(-беск, 0)U(3/4,+беск)
Похожие вопросы
Предмет: Алгебра,
автор: alinadenisova2007
Предмет: Русский язык,
автор: valerafinnik
Предмет: Українська література,
автор: kndep7505
Предмет: Математика,
автор: мелешко14
Предмет: География,
автор: lelyaivanova6