Question

На сторонах углаАВС отмечены точки М и К так
что углы ВАК и ВСМ рвны, АВ=ВС, ВА=14, ВК=9, MС=7. найти периметр треугольника АОМ, где О точка пересечения АК и СМ.

Answer 1

Из анализа исходных данных следует, что треугольники АМО и ОКС равны. 
Решение задачи состоит из нескольких этапов:
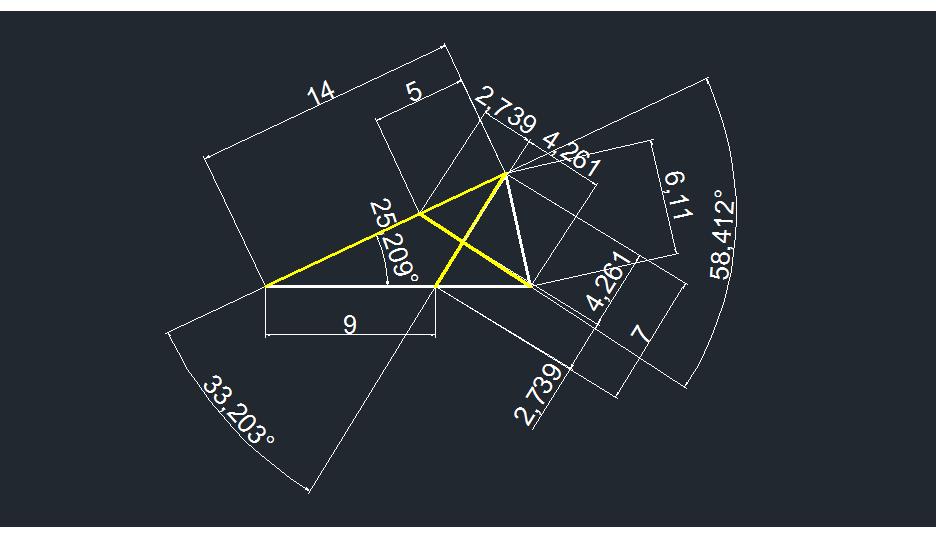
1) зная стороны треугольника АВК (14, 9 и 7) находим угол АВК по теореме косинусов - это  33,2031° и угол АВС -  25,208765°.
2) находим сторону дополнительного треугольника АВС по двум сторонам (по 14) и углу между ними (  25,208765°) - это  6,110101.
3) по сторонам треугольника АМС (5, 7 и 6,110101) по теореме косинусов находим угол АМС (он же угол АМО в заданном треугольнике -  58,41186°)
4) зная сторону АМ (5) и 2 прилежащих угла (33,2031° и 58,41186°) находим искомые стороны МО и АО -  2,7391 и 4,26087.
5) искомый периметр равен 5 +  2,7391+ 4,26087 = 12.