Question

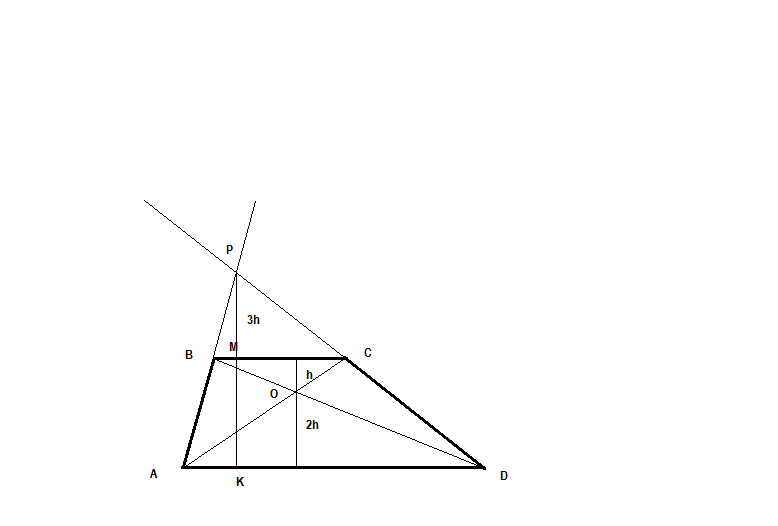
В трапеции ABCD отношение длин оснований AD и BC равно 2. Диагонали трапеции пересекаются в точке O, площадь треугольника BOC равна 3. Найдите площадь четырехугольника BOCP, где P - точка пересечения продолжений боковых сторон трапеции. Найти площадь четырёхугольника BOCP?

Answer 1

пусть h-  высота треугольника BOC

тогда 2h - высота треугольника AOD - из подобия BOC и AOD

тогда высота трапеции МК=h+2h =3h

из подобия BPC и APD следует

PK/PM = AD /BC= 2

тогда PK=6h  => РМ=3h

площадь  треугольника BOC    1/2*ВС*h= 3 (1)

площадь  треугольника BPC    1/2*ВС*3h=3*(1/2*ВС*h)= S (2)

подставим (1) в (2)   S=9

тогда

 площадь четырёхугольника BOCP  = пл  тр BOC  + пл тр BPC    = 3+9=12