Предмет: Геометрия,
автор: milkisss
РЕШИТЕ ПРАВИЛЬНО ПОЛУЧИТЕ 102 ПНК
Приложения:
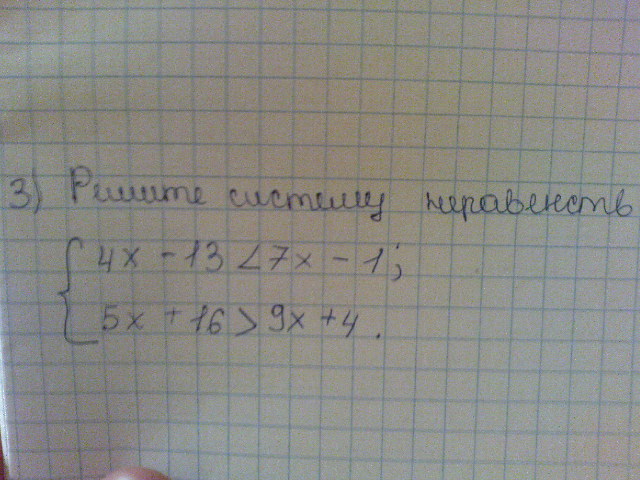


Ответы
Автор ответа:
0
решил, правильно или нет решать вам
Приложения:

Автор ответа:
0
3) 4x-13<7x-1 5x+16>9x+4
4x-7x<-1+13 5x-9x>4-16
-3x<12 -4x>-12
x>-12/3 x<12/4
x>-4 x<3
-4<x<3 (-4;3)
№) x^2-8x+16=0
x1+x2=8
x1*x2=16
x1=x2=4
1)
2)
Приложения:

Похожие вопросы