Предмет: Геометрия,
автор: Rfnhby004
Докажите, что серединный перпендикуляр к хорде окружности проходит через центр окружности
Ответы
Автор ответа:
0
Дано:
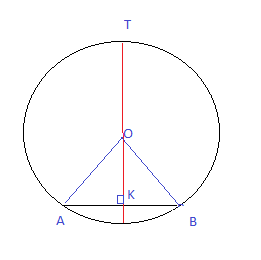
Окр(О;R), АB- хорда, АК=КВ,

Доказать: O∈KT.
Доказательство.
По определению радиуса окружности ОА=ОВ.
Характеристическое свойство серединного перпендикуляра к отрезку АВ:
все точки серединного перпендикуляра равноудалены от концов отрезка.
Точка О обладает этим свойством, значит она лежит на серединном перпендикуляре.
Окр(О;R), АB- хорда, АК=КВ,
Доказать: O∈KT.
Доказательство.
По определению радиуса окружности ОА=ОВ.
Характеристическое свойство серединного перпендикуляра к отрезку АВ:
все точки серединного перпендикуляра равноудалены от концов отрезка.
Точка О обладает этим свойством, значит она лежит на серединном перпендикуляре.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ipfgameryt
Предмет: Химия,
автор: vvikusik45
Предмет: История,
автор: romansokolov08
Предмет: Физика,
автор: Кристина060
Предмет: История,
автор: кристина5678