Предмет: Математика,
автор: kriger007
Решить неравенство 5x^2-9x-2/(x-2)(x^2-3x-4)<или равно -1
как решать методом интервалов расскажите плиз)
Ответы
Автор ответа:
0
1. Рассмотрим функцию и определим область определения функции
Знаменатель не должен равен 0
2. Определяем нули функции
Подбором: x=1
Делим
Ноли будут -3 и 2 - решено во вложения
3. Знаки на промежутке( во вложение вторая картинка)
Ответ: x ∈
Приложения:
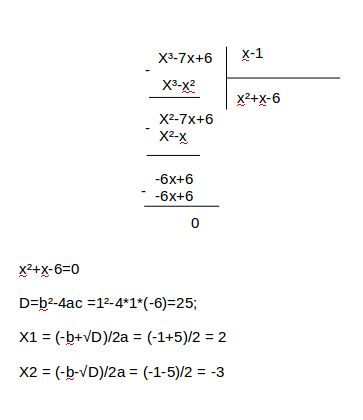
Автор ответа:
0
Жду
Автор ответа:
0
ой блин у меня 1 пропала)) x=1 ) вверху решения есть)
Автор ответа:
0
В качестве попытки упрощения выражения можно попробовать разделить числитель и знаменатель на (х-2) - подобные попытки нередко бывают успешны. Делить будем "в столбик", по правилу деления многочлена на многочлен.
Деление получилось без остатка, поэтому можно выражение сократить на (х-2), записав в ОДЗ х ≠ 2
Разложим числитель и знаменатель на множители, для чего отдельно числитель и знаменатель приравняем нулю и решим полученные квадратные уравнения.
Приходим к неравенству:
Добавляем к ОДЗ: x ≠ -1; x ≠ 4
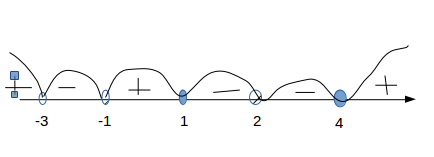
Метод интервалов заключается в следующем. Мы получили 4 точки, в которых левая часть неравенства обращается в ноль или терпит разрыв: -3; -1; 1; 4. Наносим их на числовую ось, туда же добавляем (но не рассматриваем как добавочное разбиение на интервалы) ОДЗ x ≠ 2. Не рассматриваем потому, что значение х = 2 не обращает левую часть неравенства в ноль и не является точкой разрыва.
-∞ ---------- -3 ------ (-1) ---------------- 1 ------ (2) -------------- (4) --------- +∞
Скобками показано, что точки -1, 2 и 4 являются "пробитыми", т.е. не входят в область допустимых значений переменной.
Теперь задаем значения для х на каждом полученном отрезке и проверяем знак левой части. И наносим полученные знаки на наш рисунок.
(+) (+) (+)
-∞ ---------- -3 ------ (-1) ---------------- 1 ------ (2) -------------- (4) --------- +∞
(-) (-)
Осталось выписать интервалы, где выражение в левой части меньше или равно нулю и объединить их с ОДЗ:
x ∈ [-3;-1) ∨ [1;2) ∨ (2;4)
Приложения:

Автор ответа:
0
Понимаю...Вы как всегда трудитесь во благо народа)))
Автор ответа:
0
Еще раз спасибо за подробный ответ ,Александр!
Автор ответа:
0
я?Да я просто говорю как есть
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Физика,
автор: maksimslynko4
Предмет: Русский язык,
автор: ukubaosvaasiat
Предмет: Право,
автор: ingaermune
Предмет: Обществознание,
автор: geshasnail