Question

O точка в прямоугольнике ABCD. Если АО=2м, ОС=5м, ОВ=3м, то найдите длину OD.

Answer 1

Пусть 
m - расстояние от точки О до стороны АВ
n - расстояние от точки О до стороны CD
p - расстояние от точки О до стороны ВС
q - расстояние от точки о до стороны AD.

Тогда, воспользовавшись теоремой Пифагора, имеем:
m² + q² = 2² = 4
m² + p² = 3² = 9
n² + p² = 5² = 25

OD² = q² + n² = (4 - m²) + (25 - (9 - m²) = 4+25 - 9 = 20,
и тогда OD = √20 = 2√5

Ответ: 2√5

Answer 2

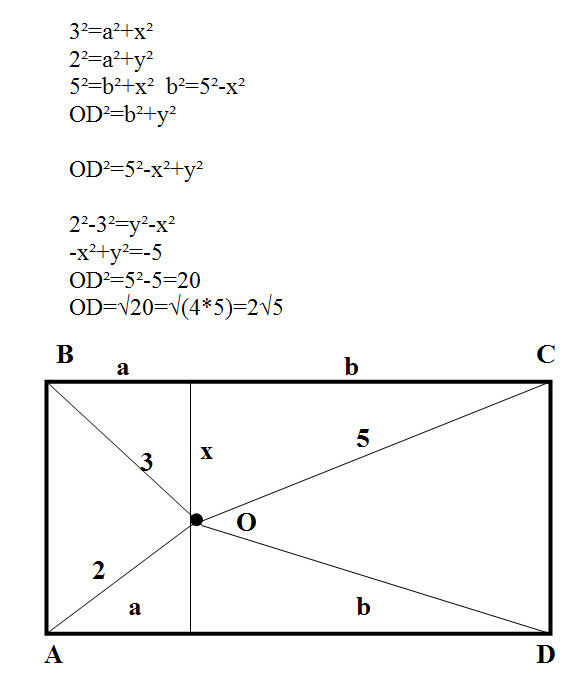
3²=a²+x²
2²=a²+y²
5²=b²+x²  b²=5²-x²
OD²=b²+y²

OD²=5²-x²+y²

2²-3²=y²-x²
-x²+y²=-5

OD²=5²-5=20
OD=√20=√(4*5)=2√5

Смотри рисунок