Предмет: Алгебра,
автор: bolela
Помогите решить задание с комплексными числами
Приложения:
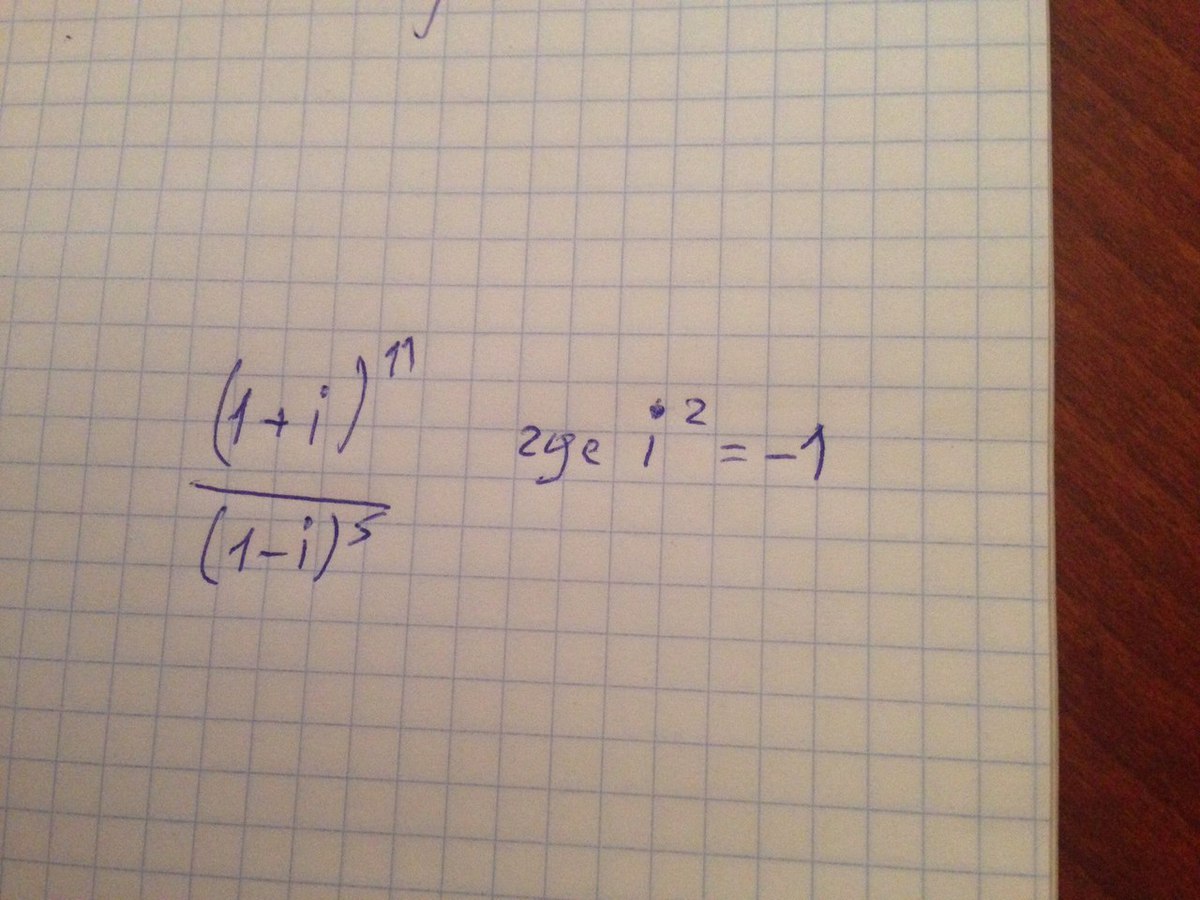
Ответы
Автор ответа:
0
решение во вложениях (в виде рисунка и в документе word)
Приложения:
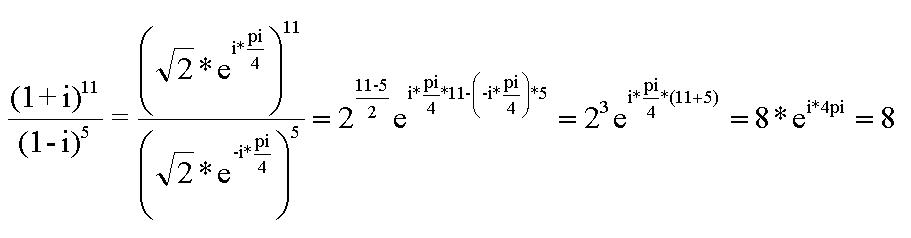
Автор ответа:
0
Можно перевести и в тригонометрическую форму:
числитель: (1 + i)^11 = (√2)^11*(cos11π/4 + i*sin11π/4) = (√2)^11*(- √2/2 + i*√2/2)
знаменатель: (1 - i)^5 = (√2)^5*(cos 5π/4 + i*sin(-5π/4) = (√2)^5*(- √2/2 + i*√2/2)
Выполняем деление: (√2)^11/(√2)^5 = (√2)^(11-5) = (√2)^6 = 8.
Ответ: 8
числитель: (1 + i)^11 = (√2)^11*(cos11π/4 + i*sin11π/4) = (√2)^11*(- √2/2 + i*√2/2)
знаменатель: (1 - i)^5 = (√2)^5*(cos 5π/4 + i*sin(-5π/4) = (√2)^5*(- √2/2 + i*√2/2)
Выполняем деление: (√2)^11/(√2)^5 = (√2)^(11-5) = (√2)^6 = 8.
Ответ: 8
Приложения:
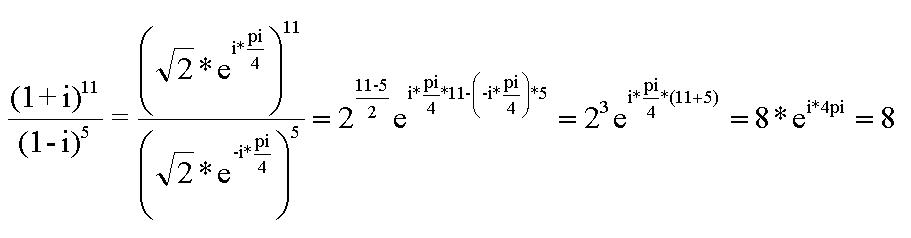
Похожие вопросы
Предмет: Физика,
автор: shkolnikdebil
Предмет: Биология,
автор: otvetteplease1
Предмет: Математика,
автор: trofimovnikita61
Предмет: Информатика,
автор: sherilusha
Предмет: Математика,
автор: катюшао