Question

  Даны
две логические функции, зависящие от трех аргументов A, B и C.


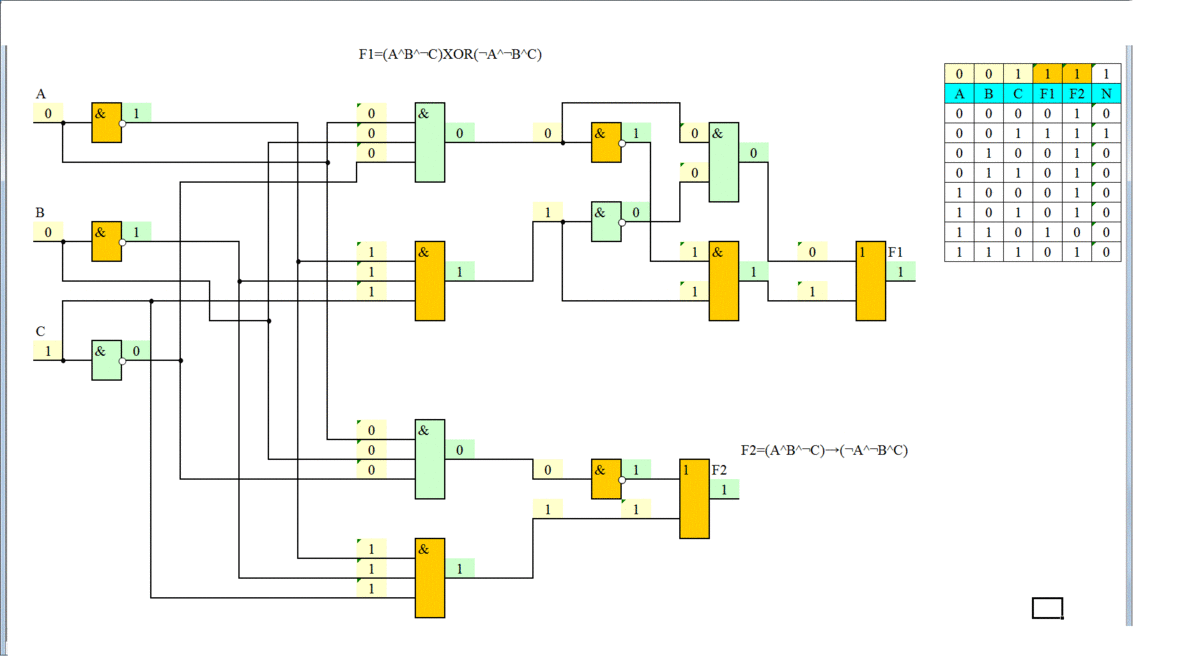
F1(A,B,C) = A and B and not C xor not A and not B and C


F2(A,B,C) = A and B and not C → not A and not B and C


Сколько существует различных комбинаций
значений A, B и C, таких, что для них:

F1(A,B,C) = F2(A,B,C)?
---------------------------
Сократил первое по СДНФ, получилось то же самое что и дано в условии, второе сократилось по СКНФ до not A or not B or C

Answer 1

У меня получилось 1 решение при 001
_______________

409b91cd289c23ca353b85cac1c7acea.xls

Answer 2

F2=(A^B^¬C)→(¬A^¬B^C)
F2 = (¬A·¬B·¬C)v(¬A·¬B·C)v(¬A·B·¬C)v(¬A·B·C)v(A·¬B·¬C)v(A·¬B·C)v(A·B·C)
F2 = (¬A·¬B)v(¬A·B)v(A·¬B·¬C)v(A·C)
F2 = ¬Av(A·¬B·¬C)v(A·C)
F2 = ¬Av(A·¬B·¬C)v(A·C)
F2=¬AvA^¬BvA^C

Answer 3

как у вас импликация вначале дала такую длинну цепочку уравнения?

Answer 4

а в первом исключающее или просто поставило отрицание над всем примером

Answer 5

Извиняюсь, тупанул, понял про первое уравнение, но со вторым не могу разобраться