Предмет: Геометрия,
автор: zhenya1201
Биссектрисы углов C и D параллелограма ABCD пересекаются в точке K стороны AB.Докажите что K- середина AB.
Ответы
Автор ответа:
0
Решение задачи:∠CDK=∠AKD (т.к. это накрест-лежащие углы).
Так как DK - биссектриса, то:
∠CDK=∠ADK.
Получается, что треугольник AKD - равнобедренный (по свойству равнобедренного треугольника).
Тогда, по определению равнобедренного треугольника:
AD=AK.
∠DCK=∠CKB (т.к. это накрест-лежащие углы).
Так как CK - биссектриса, то:
∠DCK=∠KCB.
Получается, что треугольник CKB - равнобедренный (по свойству равнобедренного треугольника)
Тогда, по определению равнобедренного треугольника:
BC=BK.
AD=BC (по свойству параллелограмма), следовательно:
AK=KB
Так как DK - биссектриса, то:
∠CDK=∠ADK.
Получается, что треугольник AKD - равнобедренный (по свойству равнобедренного треугольника).
Тогда, по определению равнобедренного треугольника:
AD=AK.
∠DCK=∠CKB (т.к. это накрест-лежащие углы).
Так как CK - биссектриса, то:
∠DCK=∠KCB.
Получается, что треугольник CKB - равнобедренный (по свойству равнобедренного треугольника)
Тогда, по определению равнобедренного треугольника:
BC=BK.
AD=BC (по свойству параллелограмма), следовательно:
AK=KB
Приложения:
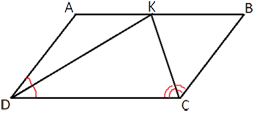
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Физика,
автор: ajdarovaz796
Предмет: Математика,
автор: dauyrhanovaakniet
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: nansyf