Question

13. Докажите, что если диагонали трапеции перпендикулярны, то сумма квадратов их длин равна квадрату суммы длин оснований

Answer 1

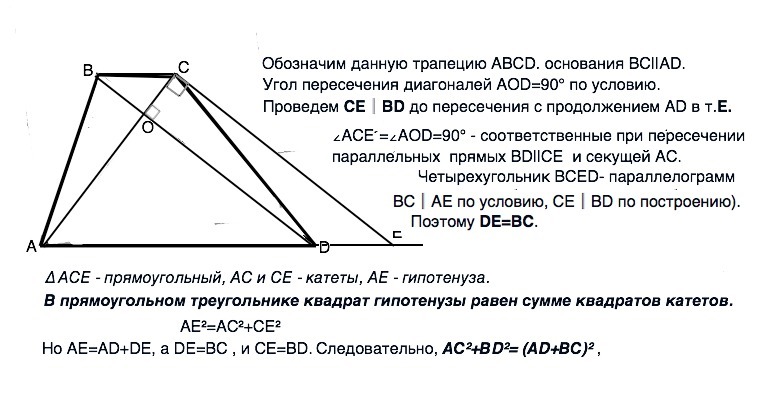
Обозначим данную трапецию АВСD. основания ВС║AD.

 О- точка пересечения диагоналей, ∠АОD=90° по условию.

Проведем СЕ║ВD до пересечения с продолжением АD в т.Е.

∠АСЕ =∠АОD=90° - соответственные при пересечении параллельных  прямых BD||СЕ  и секущей АС. 

Четырехугольник ВСЕD- параллелограмм ( противоположные стороны ВС║АE по условию, СЕ║BD по построению). Поэтому DE=ВС.

∆ АСЕ - прямоугольный, АС и СЕ - катеты, АЕ - гипотенуза. 

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 

АЕ²=АС²+СЕ²

Но АЕ=AD+DE, а DE=BC , и СЕ=ВD. Следовательно, 

Сумма квадратов диагоналей АС²+ВD²= (АD+ВС)² (квадрату суммы оснований) , что  и требовалось доказать.