Предмет: Физика,
автор: macoka
По двум бесконечно
длинным прямым параллельным проводникам, расстояние между которыми
d = 20 см, текут токи I1 = 40 А и
I2 = 80 А в одном направлении. Определить магнитную
индукцию B в точке A, удаленной от первого проводника на
R1 = 12 см и от второго на R2 = 16 см.
Ответы
Автор ответа:
0
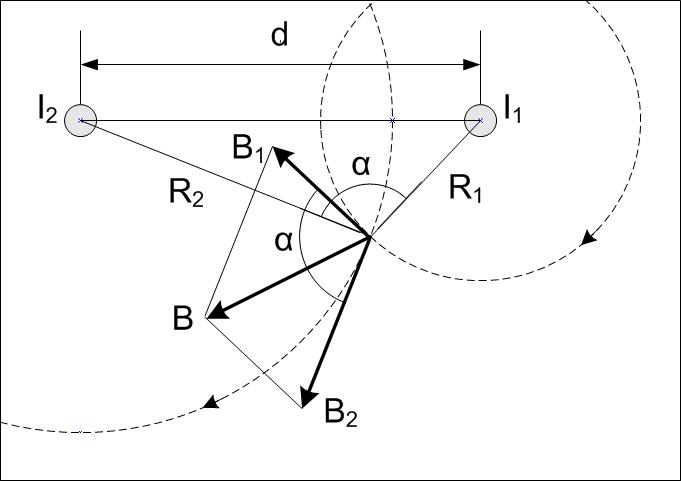
На чертеже представлена схема с поперечным сечением проводников, в которой токи идут "от нас". Направления векторов индукции B1 и В2 определяем по правилу буравчика, В - искомая сумма векторов (на основании принципа суперпозиции). Из теоремы косинусов определяем модуль B:

В треугольнике, вершинами которого являются оси проводников с током и точка, в которой ищется магнитная индукция, угол "альфа" равен углу между векторами В1 и В2 (легко доказывается из чертежа). Это угол можно определить также по теореме косинусов:

По закону Био-Савара-Лапласа определим модули векторов напряженности В1 и B2:

Ответ: 0.00012 Тл
В треугольнике, вершинами которого являются оси проводников с током и точка, в которой ищется магнитная индукция, угол "альфа" равен углу между векторами В1 и В2 (легко доказывается из чертежа). Это угол можно определить также по теореме косинусов:
По закону Био-Савара-Лапласа определим модули векторов напряженности В1 и B2:
Ответ: 0.00012 Тл
Приложения:
Похожие вопросы
Предмет: Химия,
автор: perizatkalymzanova3
Предмет: Физика,
автор: nasty2448
Предмет: Қазақ тiлi,
автор: sayyorasweet
Предмет: Алгебра,
автор: олькааааа
Предмет: Алгебра,
автор: Эми232