Предмет: Алгебра,
автор: MariaB31
помогите пожалуйста....Очень срочно! пожалуйста
5^(2x+5)*9^(2-x)*64^(x+1)=600^(4x+1)
Приложения:
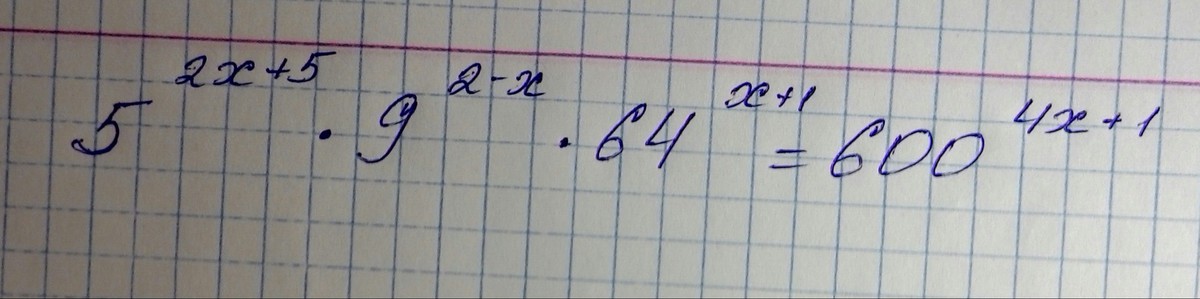
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Информатика,
автор: elennavikyan2369
Предмет: Русский язык,
автор: uenikr
Предмет: Химия,
автор: rus16852
Предмет: Физика,
автор: jeka39
Предмет: История,
автор: Alyenka