Предмет: Математика,
автор: federko1996
Решите неравенство log1-x (3x^2-x)больше либо равно2
Ответы
Автор ответа:
0
Находим область определения
Выражение под логарифмом должно быть положительным:
3x²-x>0
Находим корни
3x²-x=0
x(3x-1)=0
x₁=0
3x-1=0
x₂=1/3
Графически это парабола. Ветви вверх. Она положительна при x∈(-∞;0)U(1/3;∞)
Основание логарифма также должно быть положительным и неравным 1
1-x>0
x<1
1-x≠1
x≠0
Окончательно, область определения: x∈(-∞;0)U(1/3;1)

Решаем уравнение

Определяем знаки полученных интервалов
1) x=-2

2) x=-0.5

3) x=0.4

4) x=0.8

+ - + -
/////////////////*/////////////₀---------------₀///////*/////////₀-------------------->
-1 0 1/3 0.5 1
В ответ выписываем положительные
Ответ: x∈(-∞;-1)U(1/3;0.5)
Выражение под логарифмом должно быть положительным:
3x²-x>0
Находим корни
3x²-x=0
x(3x-1)=0
x₁=0
3x-1=0
x₂=1/3
Графически это парабола. Ветви вверх. Она положительна при x∈(-∞;0)U(1/3;∞)
Основание логарифма также должно быть положительным и неравным 1
1-x>0
x<1
1-x≠1
x≠0
Окончательно, область определения: x∈(-∞;0)U(1/3;1)
Решаем уравнение
Определяем знаки полученных интервалов
1) x=-2
2) x=-0.5
3) x=0.4
4) x=0.8
+ - + -
/////////////////*/////////////₀---------------₀///////*/////////₀-------------------->
-1 0 1/3 0.5 1
В ответ выписываем положительные
Ответ: x∈(-∞;-1)U(1/3;0.5)
Автор ответа:
0
Без фото трудно понять.Я решала так, как поняла условие.
Приложения:
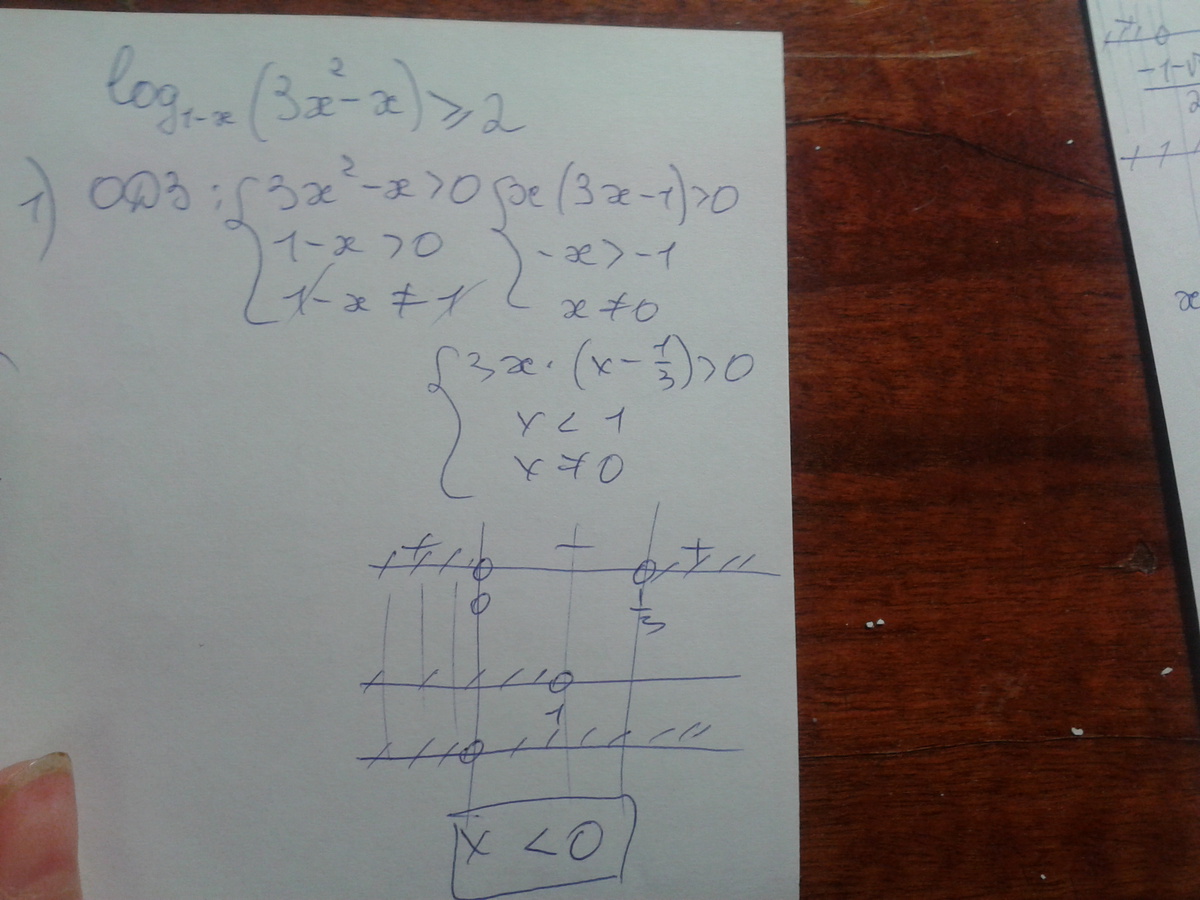


Похожие вопросы
Предмет: История,
автор: zarabaron
Предмет: Математика,
автор: salman23
Предмет: Математика,
автор: nurovamilana
Предмет: Математика,
автор: yuliachaki
Предмет: Химия,
автор: aleksatekila