Question

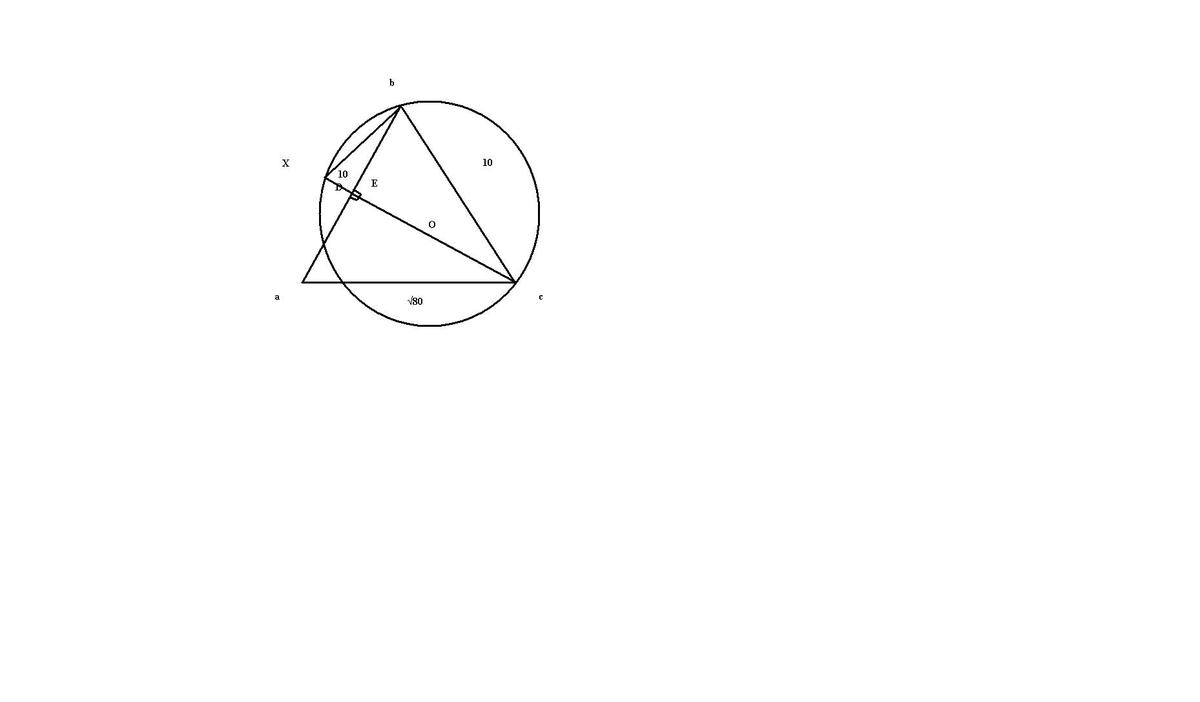
Дан равнобедренный треугольник abc с боковыми сторонами ab = bc = 10 и основанием ac = корень из 80. Найти радиус окружности, проходящей через вершины B и С центр которой находится на высоте CD.

Можете показать как будет выглядеть чертеж?

Answer 1

Найдем площадь треугольника  
$S=frac{sqrt{80}sqrt{10^2-frac{80}{4}}}{2}=40\ S=frac{AB*CD}{2}=40\ CD=8$ 
Высота равна $8$. Достроим  треугольник $XBC$ , угол $XBC$ $90а$ , так как  $XC$ диаметр окружности . 
Найдем угол $80=2*10^2-2*10^2*cosABC\ cosABC=frac{3}{5}$. 
Тогда угол $XBE=90-arccos(frac{3}{5})$. 
$BD=sqrt{10^2-8^2}=6$. 
$XB=frac{6}{sin(arccosfrac{3}{5})}\ sina=frac{4}{5}\ XB=frac{6}{frac{4}{5}} = frac{15}{2}\ XE=sqrt{(frac{15}{2})^2-6^2}=frac{9}{2}\ XC=frac{9}{2}+8=frac{25}{2}$
Тогда радиус    $R=frac{25}{4}$.