Предмет: Алгебра,
автор: abdullagazgire
Решите задачу. Расстояние от центра основания конуса до середины образующей равно 4 см, а угол наклона образующей конуса к плоскости основания равен 60 градусов. Найдите площадь осевого сечения конуса.
Ответы
Автор ответа:
0
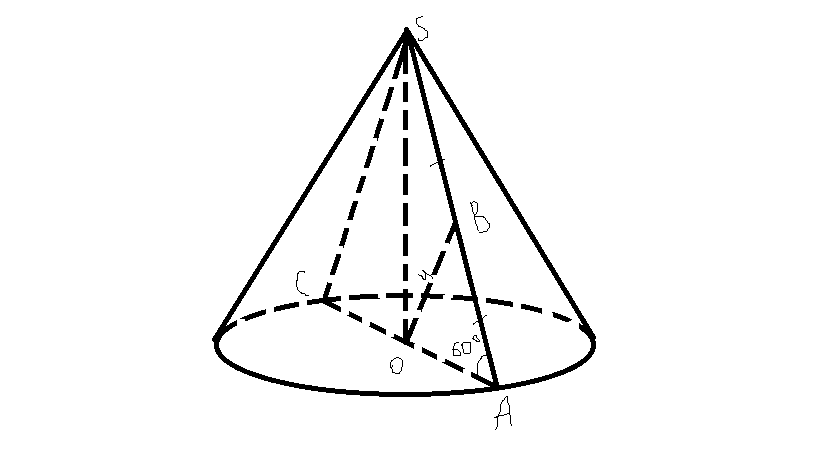
Дано: конус, AB=BS, BO=4см, угол OAS=60°, ΔACS - осевое сечение конуса
Найти: SΔACS
Решение:
1) B - средина AS
О - средина AC
BO - средняя линия ΔACS
CS=2BO=2*4=8 (см)
2) AS=CS=8 см
3) Из ΔAOS: угол AOS=90°
 (см)
(см)
 (см)
(см)
4) AC=2AO=2*4=8 (см)
5) (см²)
(см²)
Найти: SΔACS
Решение:
1) B - средина AS
О - средина AC
BO - средняя линия ΔACS
CS=2BO=2*4=8 (см)
2) AS=CS=8 см
3) Из ΔAOS: угол AOS=90°
4) AC=2AO=2*4=8 (см)
5)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: sasahametova
Предмет: История,
автор: n2687
Предмет: Другие предметы,
автор: samsatovaguli
Предмет: Химия,
автор: Илона1996
Предмет: Биология,
автор: 230201