Question

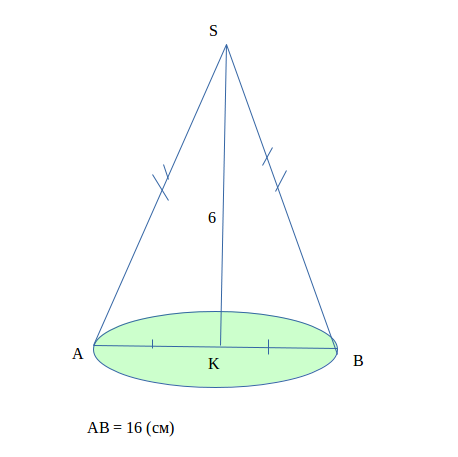
Конус. Высота 6 см, диаметр основания 16 см. Найдите площадь боковой поверхности

Answer 1

Sбок=$pi Rl$
D=16,тогда R=8
По теореме Пифагора:
$l= sqrt{ h^{2}+ R^{2} } = sqrt{36+64} = sqrt{100} =10$
Sбок=$pi *8*10=80 pi$ см²

Answer 2

Дано:

ASB - конус, AS = SB - образующая, SK = 8 (см), AB = 16 ( см ), AK = BK -  радиус основания.

Найти: S(бок).

                                       Решение:

Радиус основания в два раза меньше диаметра AB

AK = AB/2 = 16/2 = 8 (см).

С прямоугольного треугольника SKA

AS² = AK²+SK²

AS = √(AK²+SK²) = √(8²+6²)=√100 = 10 (см).

Теперь площадь боковой повехности

S(бок) = π*r*l=π*8*10 = 80π (см²).

Ответ: 80π (см²).