Предмет: Математика,
автор: awenlime
помогите пожалуйста решить log0,5х>log2(3-2х)
Ответы
Автор ответа:
0
ОДЗ
3-2x>0
x<0,5

с учетом одз
x∈(0;0,5)
3-2x>0
x<0,5
с учетом одз
x∈(0;0,5)
Автор ответа:
0
чертеж графиков в приложении
Приложения:
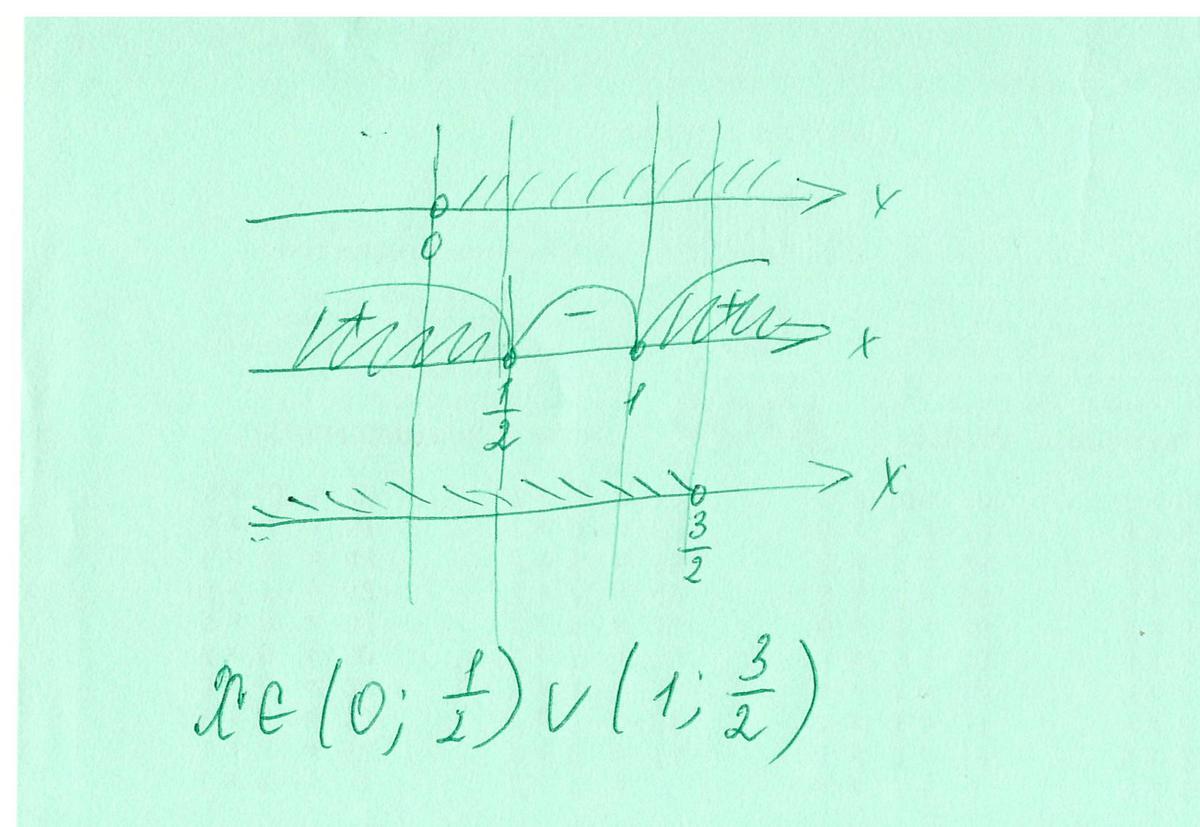
Похожие вопросы
Предмет: Химия,
автор: kalykovaaibala
Предмет: Английский язык,
автор: beka22318
Предмет: Математика,
автор: Krein4
Предмет: Информатика,
автор: Аноним