Question

в прямоугольном треугольнике гипотенуза bc равна 20, катет
ab равен 16 найдите квадрат расстояния от вершины a до биссектрисы угла c

Answer 1

В прямоугольном треугольнике гипотенуза BC равна 20, катет AB равен 16. Найдите квадрат расстояния от вершины A до биссектрисы угла C.

Расстояние от точки до прямой измеряется перпендикуляром, проведенным от этой точки до прямой.
Сделаем рисунок. 
Пусть биссектриса угла С будет СК.
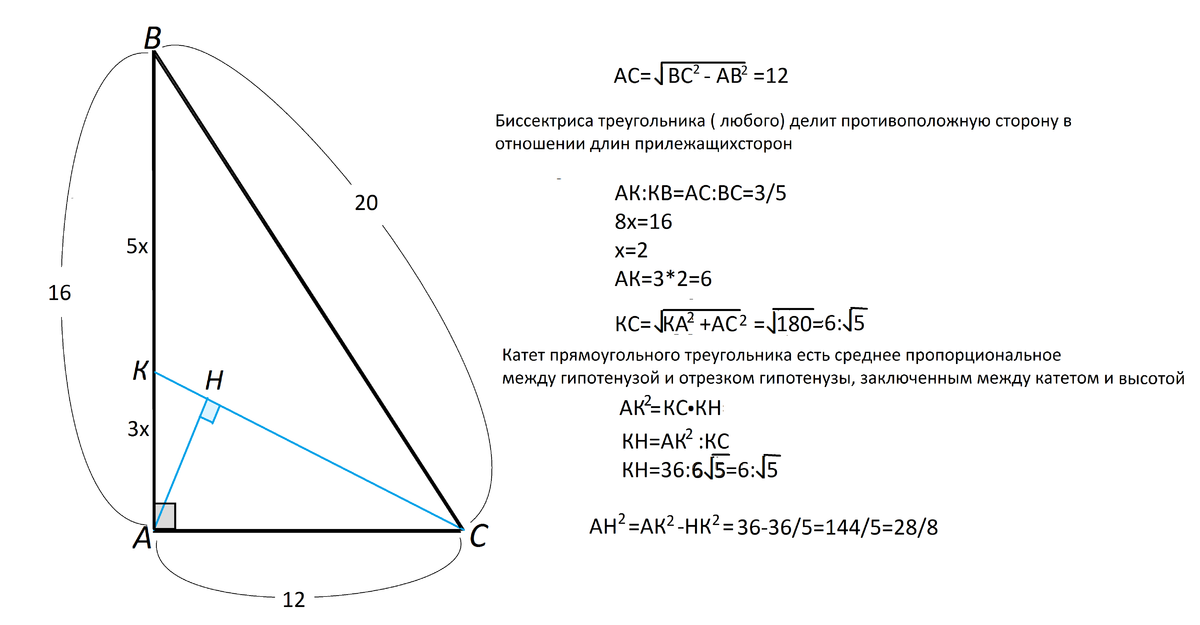
Биссектриса треугольника (любого) делит противоположную сторону в 
отношении длин прилежащих сторон.
⇒ АК:КВ=АС:ВС=12:20=3/5
⇒АК=АВ:(3+5)*3
АК=6
Рассмотрим ⊿КАС
КС - гипотенуза 
КС=√(АК²+АС²)=√180=6√5
АН можно найти из ⊿АНК.
Катет прямоугольного треугольника есть среднее пропорциональное
 между гипотенузой и отрезком гипотенузы, заключенным между катетом высотой
АК²=КН*КС
36=КН*6√5
КН=36:6√5=6:√5
АН²=АК²-КН²
АН²=36-(36:5)=144/5=28,8
Ответ: квадрат расстояния от вершины A до биссектрисы угла C равен 28,8