Предмет: Математика,
автор: yokii
найти уравнение касательной к циклоиде x = a·(t – sin t), y = a·(1 – cost) в точке М (a(pi/2-1); a)
Ответы
Автор ответа:
0
dy/dx=(dy/dt)/(dx/dt) = (a*sin(t))/(a·(1 – cos( t))= sin(t)/(1 – cos( t))
dy/dx= sin(t)/(1 – cos( t))
М (a(pi/2-1); a) = М (x(t=pi/2);y(t=pi/2))
dy/dx(t=pi/2) = sin(pi/2)/(1 – cos(pi/2)) = 1
искомая касательная имеет вид
y-y0 = dy/dx * (x-x0)
y-a = 1 * (x-a(pi/2-1))
y=a + x-a(pi/2-1)
y=x+a*(2-pi/2)-это ответ
*****************
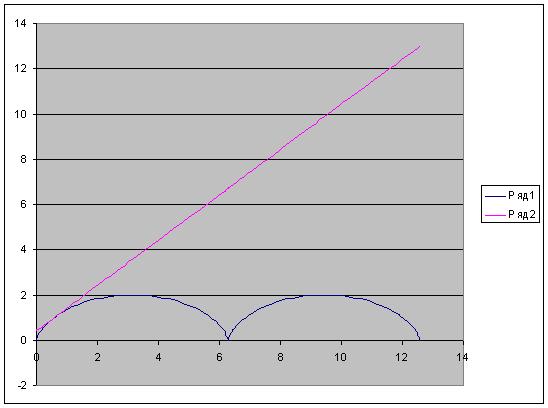
во вложении график при а=1
dy/dx= sin(t)/(1 – cos( t))
М (a(pi/2-1); a) = М (x(t=pi/2);y(t=pi/2))
dy/dx(t=pi/2) = sin(pi/2)/(1 – cos(pi/2)) = 1
искомая касательная имеет вид
y-y0 = dy/dx * (x-x0)
y-a = 1 * (x-a(pi/2-1))
y=a + x-a(pi/2-1)
y=x+a*(2-pi/2)-это ответ
*****************
во вложении график при а=1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: aglinskay
Предмет: Английский язык,
автор: verasolovovo
Предмет: История,
автор: nloor37
Предмет: Алгебра,
автор: lololo310500
Предмет: Математика,
автор: Olga5list