Предмет: Алгебра,
автор: homenkodima
Помогите решить уравнение срочно 2Cos^2x-Sin^2x=0
Ответы
Автор ответа:
0
вроде так...удачи вам
Приложения:
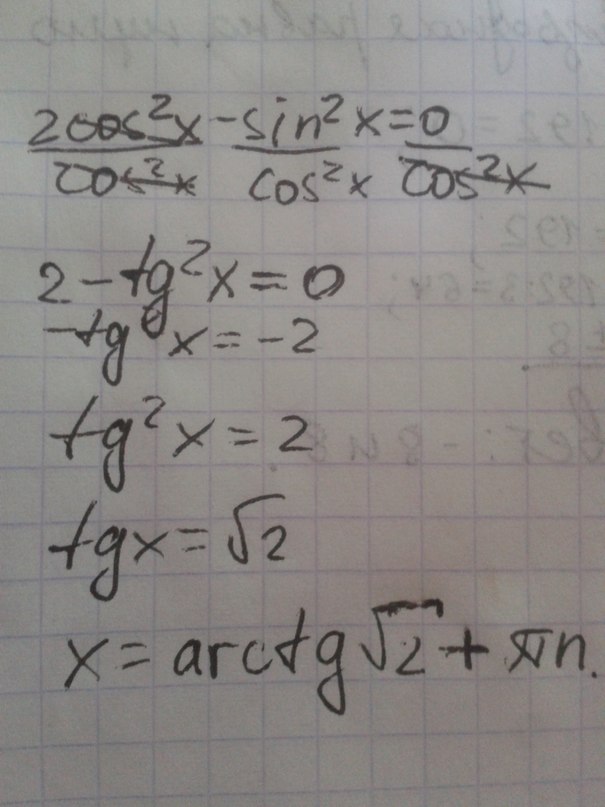
Автор ответа:
0
Можно решить другим способом, зная основное тригонометрическое тождество, и затем - подстановкой.
Основное тригонометрическое тождество имеет вид:

Откуда выражая косинус или синус приходим к такому выражению. Я выражаю синус.

Подставляю в наш пример:

Далее используем формулу понижения степени. Для косинуса имеет вид:

Для нашего уравнения:

Основное тригонометрическое тождество имеет вид:
Откуда выражая косинус или синус приходим к такому выражению. Я выражаю синус.
Подставляю в наш пример:
Далее используем формулу понижения степени. Для косинуса имеет вид:
Для нашего уравнения:
Приложения:
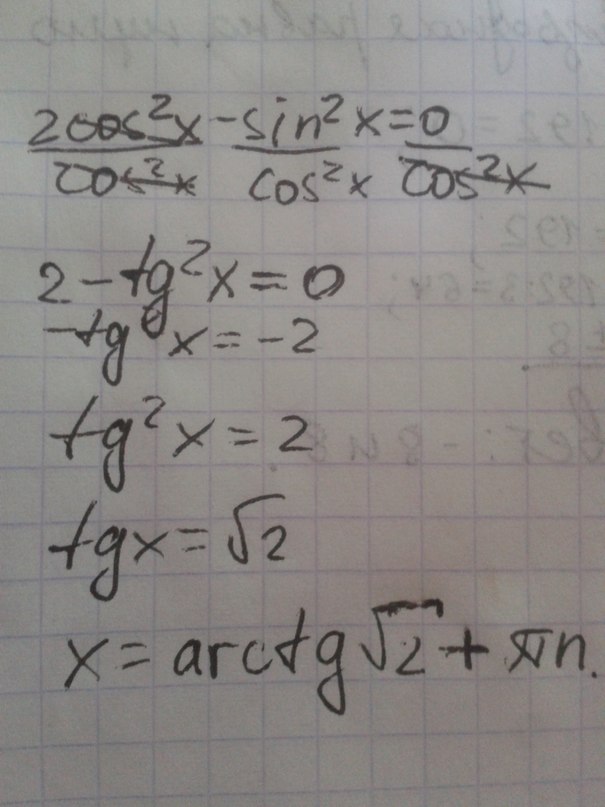
Похожие вопросы
Предмет: Математика,
автор: amaliamamedtohdieva
Предмет: Алгебра,
автор: doroniniarosjlav74
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: sabir1111
Предмет: Физика,
автор: kristyanka228