Question

ПОМОГИТЕ ПОЖАЛУЙСТА 
радиус основания конуса равен 10 см а образующая наклонена к плокоти основания под углом 45 градусов найдите площадь сечения проходящего через две образующие угол между которыми равен 30 градусов и площадь боковой поверхности конуса

Answer 1

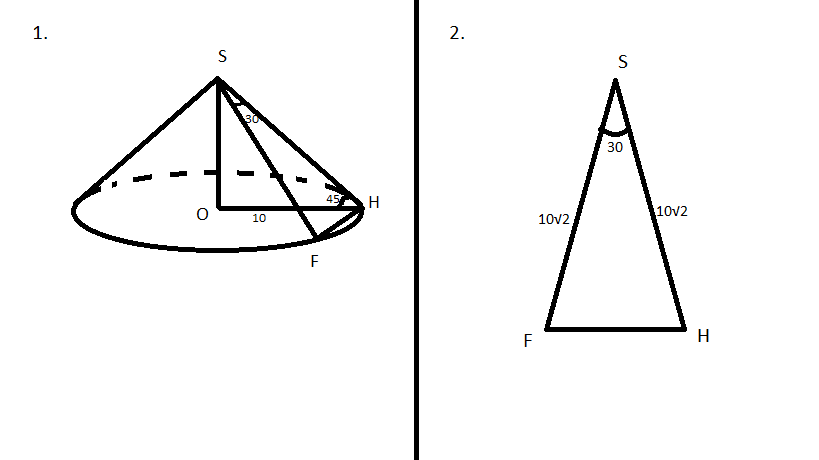
1) Начнем с площади боковой поверхности.
Рассмотрим ΔSOH.
угол S = 180 - (90+45) = 45 градусов
ΔSOH - равнобедренный.(так как углы при основании равны) ⇒ OH = SO = 10 см
SH² = SO² + OH²  (по т. Пифагора)
SH(образующая) = √ 100 + 100 = √200 = 10√2 см 
Sбок. = π * r * l = 100√2 cm²
__________________________

2) Рассмотрим ΔSHF.
ΔSHF - равнобедренный (т.к. SH = SF = 10√2)
S = 1/2 * a * b * sinα
S = 1/2 * 10√2 * 10√2 * sin30
S = 1/2 * 200 * 1/2 = 50 cm²
__________________________
Ответы выделил жирным курсивом.
Рисунок во вложении)