Question

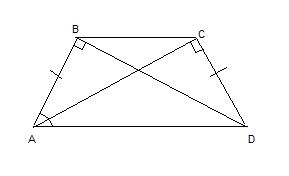
В равнобокой трапеции ABCD диагональ АС перпендикулярна CD и является биссектрисой угла А. Найдите угол DAB.

Answer 1

<BCA=<CAD как накрест лежащие углы при пересечении двух параллельных прямых ВС и AD секущей АС.
Но<BAC=<CAD, т.к. АС - биссектриса. Значит <BCA=<BAC, и треугольник АВС - равнобедренный (углы при его основании АС равны). АВ=ВС.
Поскольку трапеция равнобедренная, то и ВС=CD, треугольник BCD также равнобедренный и равный треугольнику АВС (они равны по двум сторонам и углу между ними. АВ=ВС=CD, <ABC=DCB, т.к. трапеция равнобедренная).
Пусть угол ВАС будет х. Тогда углы BAD и CDA будут 2х, углы АВС и DCB будут 90+х. Зная сумму углов 4-угольника, запишем:
<BAD+<ABC+<DCB+<CDA=360
2х+(90+х)+(90+х)+2x=360
6x+180=360
6x=180
x=30
<DAB=2*30=60°