Предмет: Геометрия,
автор: zubareffnikita
основания равнобедренной трапеции равны 14 и 50 боковая сторона равна 30.найдите длину диагонали трапеции.
Ответы
Автор ответа:
0
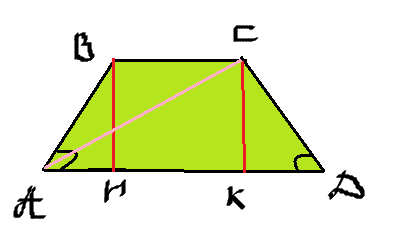
Рисунок смотрите во вложения.
Дано:
ABCD - равнобедренная трапеция, угол A = углу D = 30 градусов, BH и CK - высоты, AB = CD = 30 (см). AD || BC, BC = 14 (см), AD = 50 (см).
Найти: AC.
Решение:
1.Проведём высоты BH и CK, следовательно найдём AH
AH = (AD-BC)/2 = (50 - 14) /2 = 36/2=18 (см).
2. С прямоугольного треугольника ABH (угол AHB = 90градусов):
AH = 18 (см), AB = 30 (см), угол А =30градусов.
Определяем высоту BH.
За т. Пифагора
AB² = AH² + BH²
BH² = AB² - AH²

3. Определяем Диагональ АС.
С прямоугольного треугольника ACK (угол AKC = 90градусов)
За т. Пифагора

Ответ: AC = 40 (см).
Дано:
ABCD - равнобедренная трапеция, угол A = углу D = 30 градусов, BH и CK - высоты, AB = CD = 30 (см). AD || BC, BC = 14 (см), AD = 50 (см).
Найти: AC.
Решение:
1.Проведём высоты BH и CK, следовательно найдём AH
AH = (AD-BC)/2 = (50 - 14) /2 = 36/2=18 (см).
2. С прямоугольного треугольника ABH (угол AHB = 90градусов):
AH = 18 (см), AB = 30 (см), угол А =30градусов.
Определяем высоту BH.
За т. Пифагора
AB² = AH² + BH²
BH² = AB² - AH²
3. Определяем Диагональ АС.
С прямоугольного треугольника ACK (угол AKC = 90градусов)
За т. Пифагора
Ответ: AC = 40 (см).
Приложения:
Похожие вопросы
Предмет: История,
автор: drugdrug2288
Предмет: Химия,
автор: nizamidin44
Предмет: Литература,
автор: hamitovaalisher706
Предмет: География,
автор: ArtemkaTroLoLo
Предмет: Химия,
автор: 12356654321