Предмет: Алгебра,
автор: kittycat13
Найдите все отрицательные значения параметра а, при которых система уравнений(смотри во вложениях) имеет единственное решение.
Приложения:
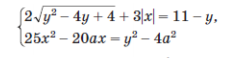
Ответы
Автор ответа:
0
Первое уравнение можно записать , и того

Рассмотрим четыре случая

По первому пункту получим
 что не отрицательное
что не отрицательное
По второму пункту получим

То есть
По третьем и четвертому пункту получим те же значения только с
Ответ
Рассмотрим четыре случая
По первому пункту получим
По второму пункту получим
То есть
По третьем и четвертому пункту получим те же значения только с
Ответ
Похожие вопросы
Предмет: Геометрия,
автор: rauschanjela
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: instadiava
Предмет: Химия,
автор: karinabuslaeva3
Предмет: Алгебра,
автор: MartinaL