Предмет: Алгебра,
автор: vladislav982
Решите неравенство
|x^2-4|(x^2-4x+3)< либо = 0
Ответы
Автор ответа:
0
Если понравилось решение - нажимай "спасибо" и "лучший" (рядом с кнопкой "спасибо") :)
Приложения:
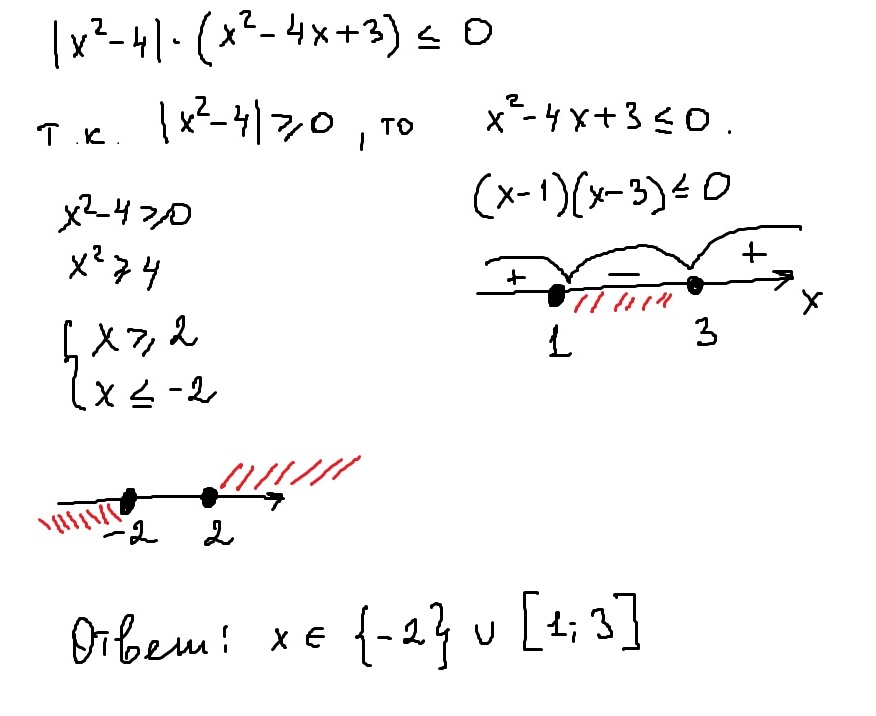
Автор ответа:
0
Вроде все нормально
Автор ответа:
0
)))))))))))
Автор ответа:
0
Вы потеряли часть решения
Автор ответа:
0
уже поняла (((((((((((((((
Автор ответа:
0
Выражение под знаком абсолютной величины всегда неотрицательно, поэтому оно не влияет на знак левой части, но может обратить левую часть в ноль, откуда получаем условие X1=-2; X2=2
Теперь рассмотрим неравенство
Разложим левую часть на множители:
Получаем неравенство (x-1)(x-3)≤0.
Рассматриваем знак выражения на интервале *****1*******3*******
Полагая х=0 находим значение: (-1)*(-3)=3 (положительное)
Полагая х=2 находим значение: 1*(-1)=-1 (отрицательное)
Полагая х=4 находим значение: 3*1=3 (положительное)
Получаем интервал ++++++ 1 ---------- 3 ++++++
Записываем область решения x∈[1;3]
Значение х2=2, найденное выше, лежит внутри этого диапазона.
Значение x1=-2 надо добавить к решению.
Окончательно х∈ -2 ∨ [1;3]
В прикрепленном файле решение компьютерной программы - для недоверчивых.
Приложения:

Автор ответа:
0
А что за фото у вас такое? что за программа? самосу прям интересно
Автор ответа:
0
У меня просто алгоритм к методу интервалу намного удобнее чем это вы дали решение.
Автор ответа:
0
Это и есть метод интервалов, только рассматривать в нем область, заданную сомножителем под знаком модуля бессмысленно: пустая трата времени. А второй сомножитель - это как раз метод интервалов. Уж не знаю, что там у Вас за "алгоритм", метод интервалов - он один и тот же всегда.
Похожие вопросы
Предмет: Английский язык,
автор: Rayanochka
Предмет: Алгебра,
автор: instadiava
Предмет: Русский язык,
автор: amirarli
Предмет: История,
автор: ivanMOHCTP