Question

Основание пирамиды-прямоугольник со сторонами 12 с и 16 см каждое боковое ребро пирамиды равно 26 см.Найдите обьём пирамиды.

Answer 1

Русь основание ABCD Найдите диагональ прямоугольника по теореме пифагора (AC=20). O- точка пересечения дианоналей, следовательно AO=OC=10 см. Рассмотрим треугольник SOC (S- вершина пирамиды). Треугольник будет прямоугольным, т.к. SO- высота. По теореме пифагора SO= 24 см. Объем пирамиды равен 1/3*S основания* высоту V=((12*16)*24)/3=1536 см кубических

Answer 2

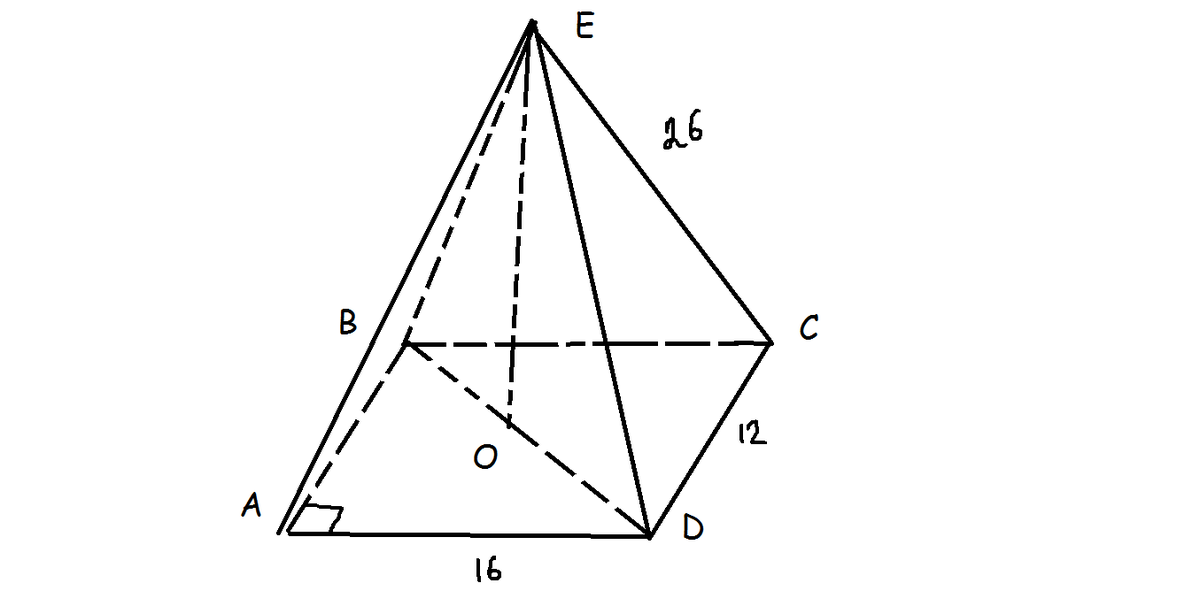
Задача имеет несколько решений, вот одно из них: (см. рисунок)
Объем пирамиды вычисляется по формуле:

$V=frac{1}3*S_{ocn}*h$

$S_{ocn}=S_{ABCD}$

$h=EO$

Найдем площадь основания.

$S_{ABCD}=AD*CD=12*16=192$

Найдем высоту:
По т.Пифагора:

$AC=sqrt{16^2+12^2}=sqrt{400}=20$

$OC=frac{AC}2=frac{20}2=10$

По т.Пифагора:

$h=sqrt{26^2-10^2}=sqrt{576}=24$

Тогда объем:

$V=frac{1}3*192*24=1536$