Предмет: Алгебра,
автор: Николай54321
Определите знак производной функции f(x) =  в указанной точке
в указанной точке 
Ответы
Автор ответа:
0
.................................
Приложения:
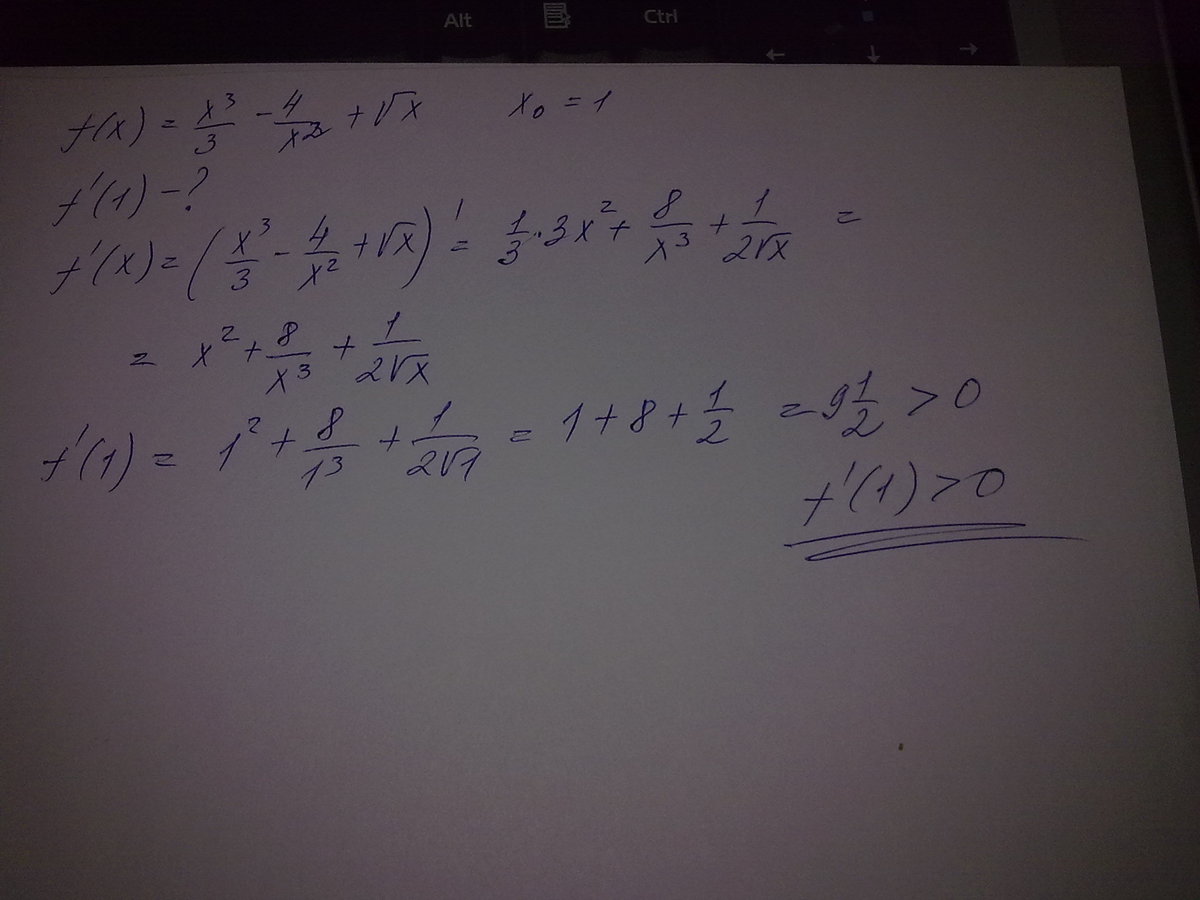
Автор ответа:
0
У Вас описка в конце вычисления производной: двойка перед радикалом в знаменателе последнего слагаемого попала в числитель и значение производной получилось неверным.
Автор ответа:
0
И еще ошибка - в производной знак перед вторым слагаемым, где 8 в числителе - положительный.
Автор ответа:
0
Производная имеет положительный знак.
Приложения:
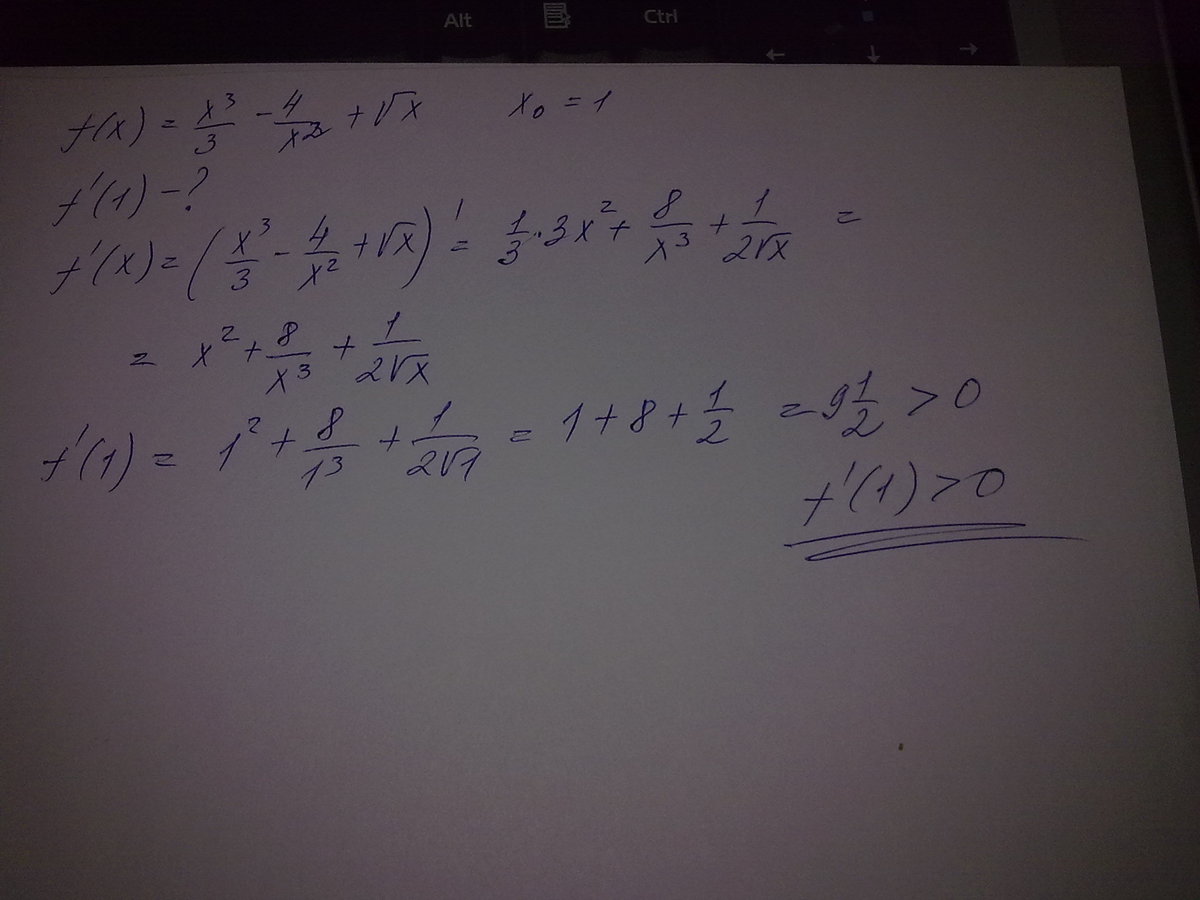
Похожие вопросы
Предмет: Алгебра,
автор: u1iana871
Предмет: Українська мова,
автор: Viva000
Предмет: Русский язык,
автор: nika03258
Предмет: Математика,
автор: arinazhakupova
Предмет: Экономика,
автор: natashabalakina