Предмет: Математика,
автор: Lina1488
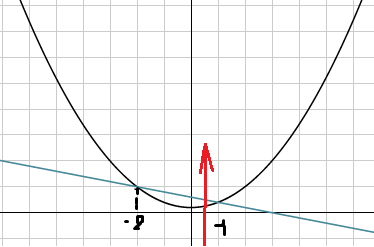
вычислить площадь фигуры,ограниченной графиками функций y=x^2+1,y=3-x
Ответы
Автор ответа:
0
y=x^2+1
y=3-x
3-x=x^2+1
3-x-x^2-1=0
-x^2-x+2=0
x^2+x-2=0
D=1+8=9
x1=-1+3/2=1
x2=-1-3/2=-2
Получили пределы интегрирования от -2 до 1
Далее нужно определить какой график будет выше
y=3-x выше значит из него и вычитаем y=x^2+1
Интеграл от -2 до 1 ((3-x)-(x^2+1) dx= (3-x-x^2-1)dx= (-x^2-x+2)dx= (-x^3/3-x^2/2+2x)=
((-(-2)^3/3-(-2)^2/2+2(-2)-(-1^3/3-1^2/2+2*1))=((-8/3-4/2+2)-(1/3+1/2+2))=-2,6-2,8=-5,4
y=3-x
3-x=x^2+1
3-x-x^2-1=0
-x^2-x+2=0
x^2+x-2=0
D=1+8=9
x1=-1+3/2=1
x2=-1-3/2=-2
Получили пределы интегрирования от -2 до 1
Далее нужно определить какой график будет выше
y=3-x выше значит из него и вычитаем y=x^2+1
Интеграл от -2 до 1 ((3-x)-(x^2+1) dx= (3-x-x^2-1)dx= (-x^2-x+2)dx= (-x^3/3-x^2/2+2x)=
((-(-2)^3/3-(-2)^2/2+2(-2)-(-1^3/3-1^2/2+2*1))=((-8/3-4/2+2)-(1/3+1/2+2))=-2,6-2,8=-5,4
Приложения:
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Информатика,
автор: Аноним
Предмет: Українська мова,
автор: vlada120908
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: robert9608