Question

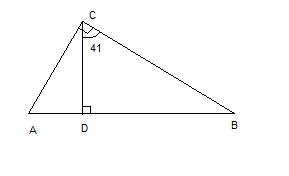
В прямоугольном треугольнике АВС где угол С равен 90 проведена высота CD угол DCB равен 41 найдите углы А В и Угол ACD.

Answer 1

<ACD = 90 - <DCB = 90 - 41 = 49°
Рассмотрим прямоугольный треуг-к ADC. Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, находим <A:
<A=90-<ACD=90-49=41°
В прямоугольном треуг-ке АВС:
<B=90-<A=90-41=49°
Можно вторым способом: треугольник ADC подобен АВС по первому признаку подобия: два угла одного треуг-ка соответственно равны двум углам другого: угол А - общий, <C=<ADC=90°. Треугольники CDB и АВС также подобны по первому признаку (угол В - общий, <CDB=<C=90°). Значит, подобны и ADC c CDB. Соответственные углы треугольников А и DCB, а также ACD и B будут равны. 
<ACD = 90 - <DCB = 90 - 41 = 49°,
<B=<ACD=49°
<A=<DCB=41°