Предмет: Математика,
автор: bastrvika
Помогите пожалуйста с решением интегралов. Хотя бы несколкьо
Приложения:
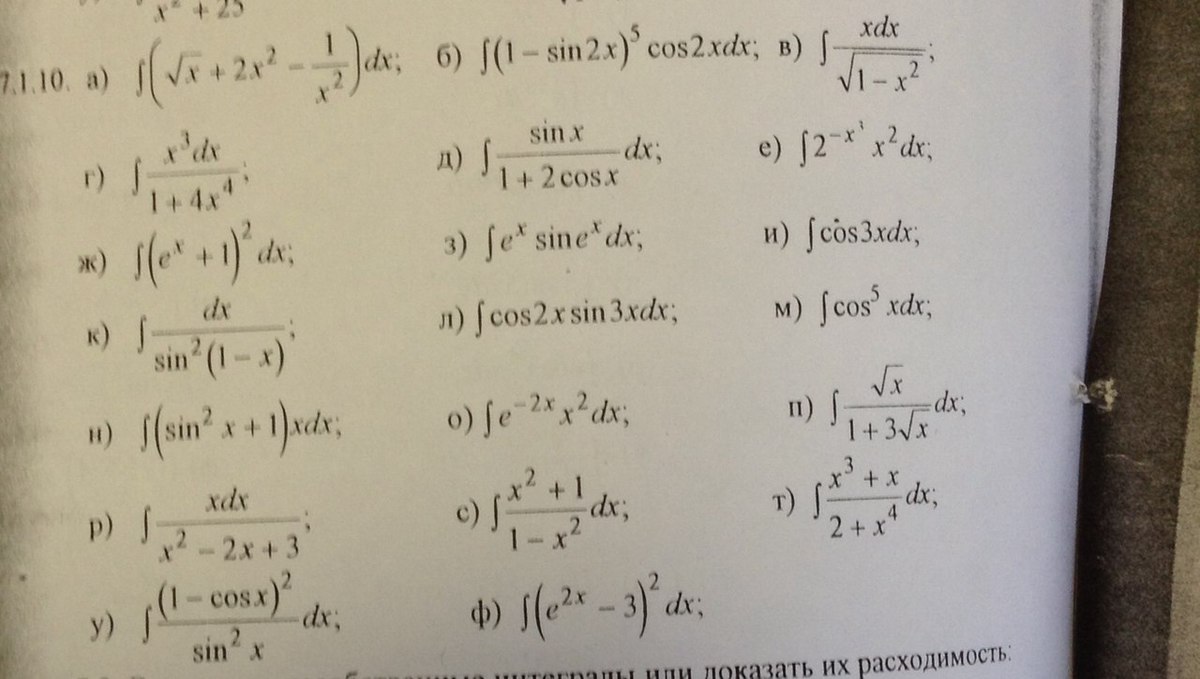
Ответы
Автор ответа:
0
Автор ответа:
0
Спасибо большущее!!
Автор ответа:
0
Там очень много примеров.Можно было бы и ещё решить, но не за 15 баллов.
Похожие вопросы
Предмет: Алгебра,
автор: magidarahatbekkyzy84
Предмет: Математика,
автор: reginochkaaa2
Предмет: История,
автор: karolinakarelina71
Предмет: Обществознание,
автор: Дашутка277