Предмет: Геометрия,
автор: Алёнка1555
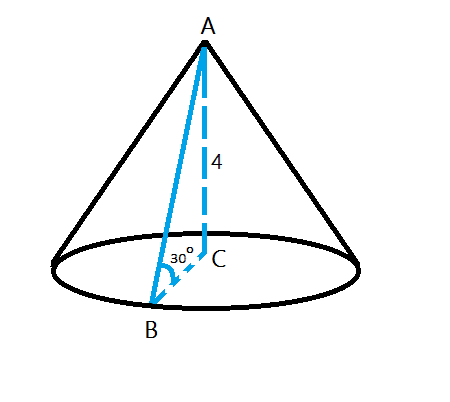
Высота конуса равна 4 см, угол наклона образующей равен 30 градусов.Найти объём конуса.
Ответы
Автор ответа:
0
r=4*tg60°=4*√3=4√3
V(конуса)=(π*r²*h)/3=(π*(4√3)²*4)/3=64π
Ответ: 64π.
V(конуса)=(π*r²*h)/3=(π*(4√3)²*4)/3=64π
Ответ: 64π.
Автор ответа:
0
Предлагаю более (ну, для меня проще решить по сторонам, чем по углам) простое решение:
Т. к. АС - высота, то ΔABC прямоугольный, угол ACB = 90°. Угол ABC = 30° как угол наклона образующей. По теореме о прямоугольном треугольнике, напротив угла в 30° лежит катет, равный половине гипотенузы. АС (катет) = 4, значит, АВ (гипотенуза) = 4*2 = 8 (см).
ВС - радиус. По теореме Пифагора находим ВС:
 (см)
(см)
 (см куб)
(см куб)
Ответ: см куб
см куб
Т. к. АС - высота, то ΔABC прямоугольный, угол ACB = 90°. Угол ABC = 30° как угол наклона образующей. По теореме о прямоугольном треугольнике, напротив угла в 30° лежит катет, равный половине гипотенузы. АС (катет) = 4, значит, АВ (гипотенуза) = 4*2 = 8 (см).
ВС - радиус. По теореме Пифагора находим ВС:
Ответ:
Приложения:
Похожие вопросы
Предмет: Физика,
автор: ivancrow228
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: pazukha2021
Предмет: Физика,
автор: ilyarusskikh