Предмет: Алгебра,
автор: mari1706
Исследовать на экстремум функцию:
y=(1/3)x^3+(1/2)x^2-2x-1/3
Определить точку перегиба и построить график функции.
Ответы
Автор ответа:
0
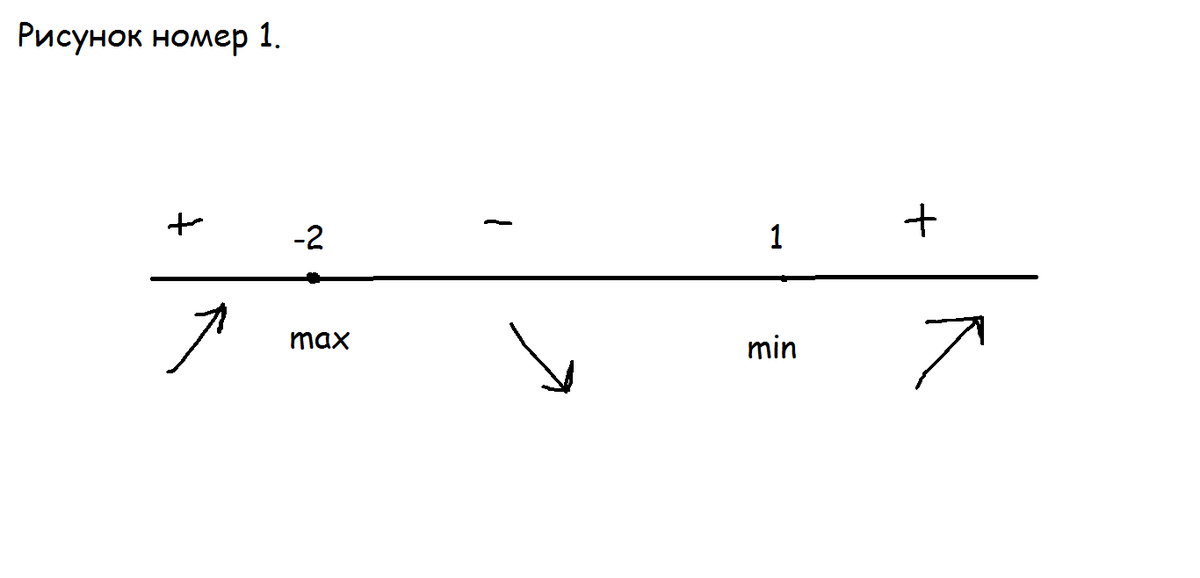
Чтобы найти экстремум функции, нужно сначала найти ее производную, и исследовать ее.
Далее см. рисунок номер 1.
И того: x=1 - точка минимума.
x=-2 - точка максимума.
Чтобы найти точки перегиба нужно найти 2-ю производную и исследовать ее график.
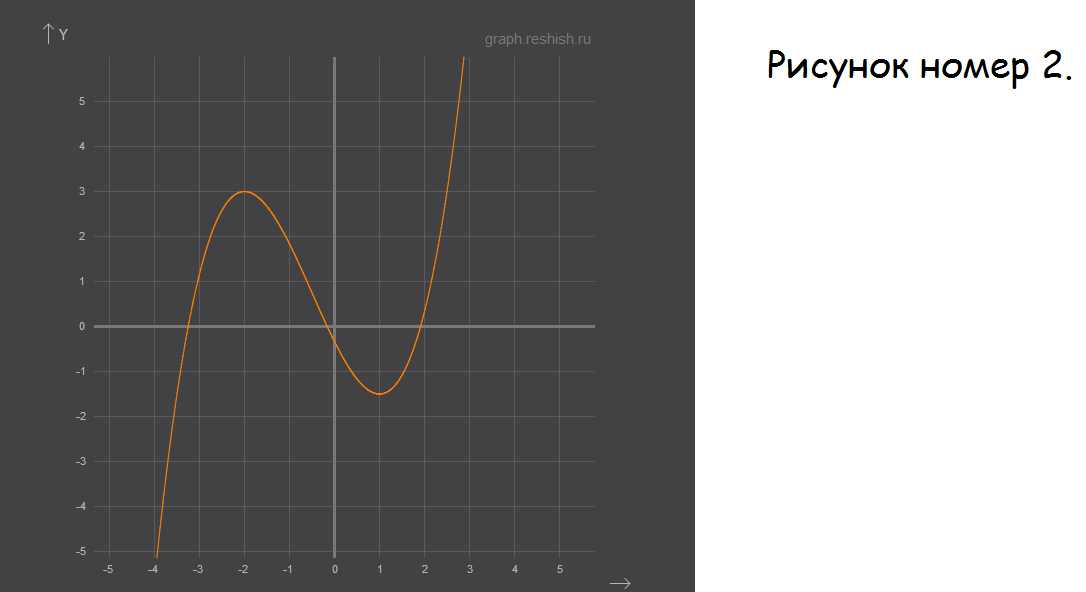
И того: точка перегиба:
Далее см. рисунок номер 2. (сам график)
Приложения:

Похожие вопросы
Предмет: Математика,
автор: asikbek16
Предмет: Химия,
автор: artem110808ttt
Предмет: Русский язык,
автор: eugenia2468000
Предмет: Физика,
автор: Angelina0808