Question

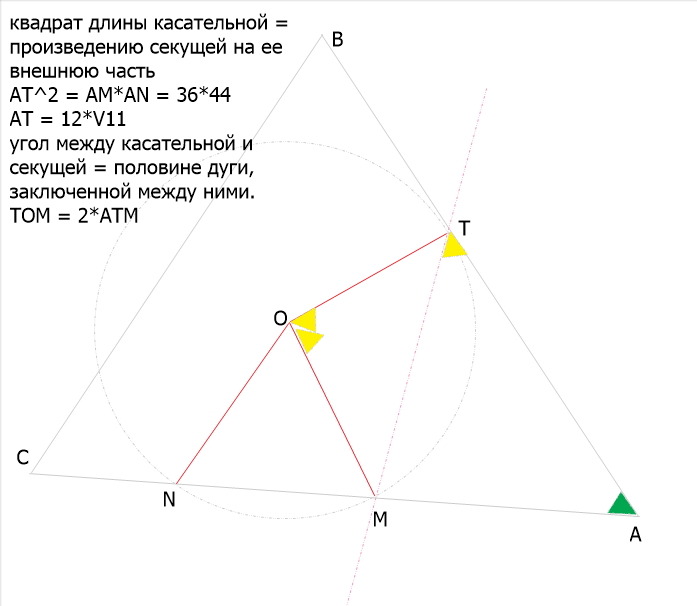
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 36 и 44 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√11/6.

Answer 1

по т.косинусов ТМ² = ТА² + МА² - 2*ТА*МА*cosBAC = 
= 36*44 + 36*36 - 2*12*√11*36*√11 / 6 = 
= 36*80 - 12*12*11 = 6*6*4*(20 - 11) = (6*2*3)²
TM = 36
треугольник ТМА -- равнобедренный и углы МТА = МАТ равны))) 
((хоть и разным цветом на рисунке отмечены)))
если в треугольнике МОТ (он равнобедренный))) провести 
высоту=медиану=биссектрису, то в получившемся прямоугольном треугольнике 
угол при вершине О будет равен углу ВАС)))
R = (TM / 2) / sinBAC = TM / (2*sinBAC)
sinBAC = √(1 - 11/36) = 5/6
R = 36*6 / 10 = 21.6