Предмет: Алгебра,
автор: darklace
Вычислить определенный интеграл (во вложении):
Приложения:
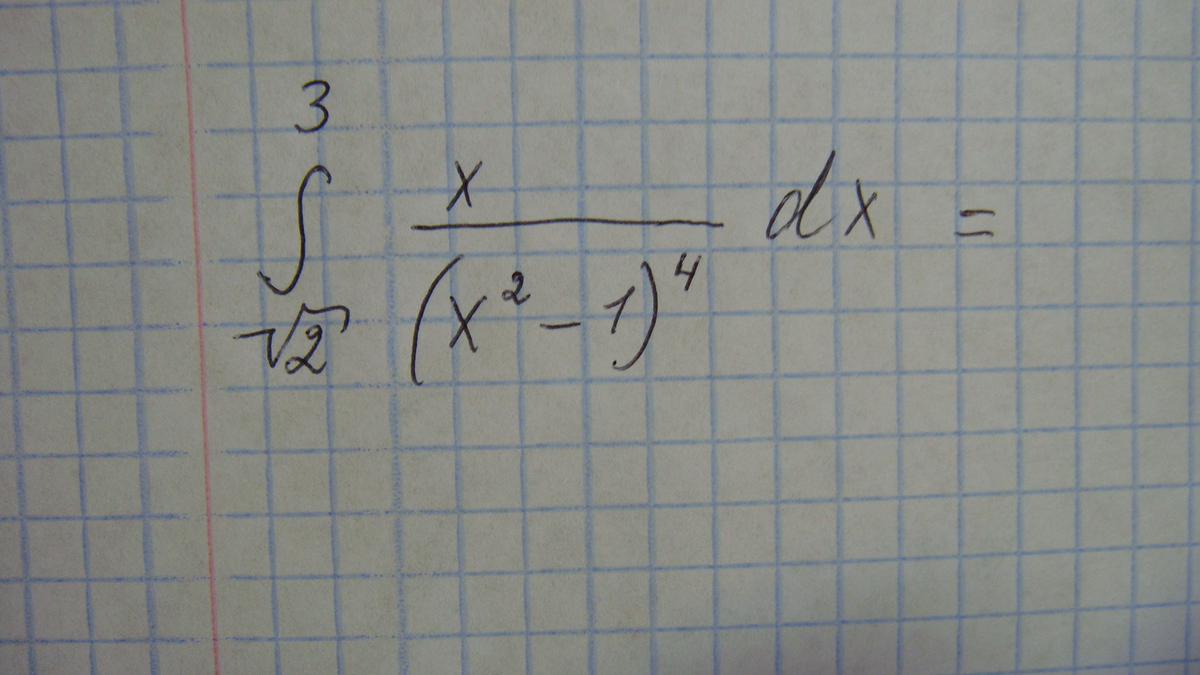
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Информатика,
автор: m4shaezhova
Предмет: Геометрия,
автор: sav4321
Предмет: Алгебра,
автор: Chiziwe