Предмет: Физика,
автор: craken3000
1.
Имеется
треугольник, собственная длина каждой стороны которого равна а. Найти периметр этого треугольника в системе отсчета, движущейся
относительно него с постоянной скоростью v вдоль одной из его сторон.
Ответы
Автор ответа:
0
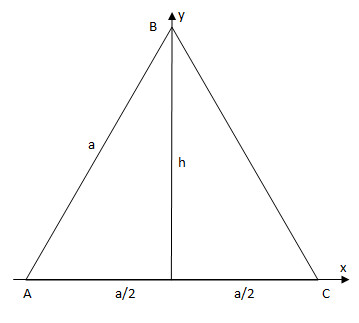
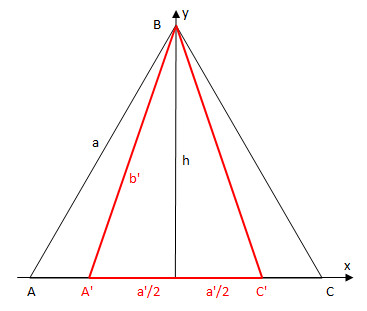
Пусть движение происходит по оси х. Тогда по оси х размеры изменяются. В направлении оси у движения нет, по ней изменения не будет. Получаем треугольник А'ВС'. Высота h не изменяется. В равностороннем треугольнике АВС угол А равен 60°. Следовательно
h=a/2*tg 60°=a√3/2
По релятивистской формуле длины (β=v/c, c - скорость света)
a'=a√(1-β²)
По т.Пифагора
b'=√(h²+(a'/2)²)=√(3a²/4+a²(1-β²)/4)=a/2*√(4-β²)
Искомый периметр:
p=a'+2b'=a√(1-β²)+a√(4-β²)=a(√(1-β²)+√(4-β²))
Ответ: a(√(1-β²)+√(4-β²)), где β=v/c
h=a/2*tg 60°=a√3/2
По релятивистской формуле длины (β=v/c, c - скорость света)
a'=a√(1-β²)
По т.Пифагора
b'=√(h²+(a'/2)²)=√(3a²/4+a²(1-β²)/4)=a/2*√(4-β²)
Искомый периметр:
p=a'+2b'=a√(1-β²)+a√(4-β²)=a(√(1-β²)+√(4-β²))
Ответ: a(√(1-β²)+√(4-β²)), где β=v/c
Приложения:
Похожие вопросы
Предмет: Психология,
автор: ewquz1on228
Предмет: Алгебра,
автор: dukefissura
Предмет: Другие предметы,
автор: alexv2009
Предмет: Литература,
автор: Аля225