Предмет: Алгебра,
автор: SleeplessNight
Писала сегодня егэ, очень уж хочется узнать, правильно ли решила)
Задание во вложении. При каких а уравнение имеет ровно два решения?
Приложения:
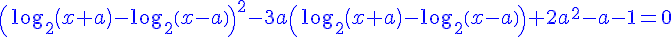
Ответы
Автор ответа:
0
замена: log(2)(x+a) - log(2)(x-a) = t
t² - 3a*t + 2a² - a - 1 = 0
D = 9a² - 8a² + 4a + 4 = (a+2)² > 0 -- условие для двух корней)))
a ≠ -2
и еще: речь про 2 корня --- для х,
значит, если выражение в первой скобке ( = t ) окажется = 0,
то второй степени для аргумента не станет и о двух корнях речи не будет...
вывод: логарифмы не должны быть равны)))
т.е. x+a ≠ x-a
0 ≠ -2a
a ≠ 0
и еще дополнение))) спасибо внимательному LNT64
в случае равенства свободного члена нулю, уравнение, конечно же, остается квадратным (относительно t ))), но становится неполным квадратным)))
и для (t) решения два, а вот для аргумента (х) -- уже нет)))
т.к. получаются равными логарифмы)))
и из условия 2а² - a - 1 ≠ 0 получим еще
а ≠ (1 +- 3) / 2
а ≠ 1
а ≠ -1/2
теперь уже вроде все)))
не зря сначала решение показалось подозрительно легким)))
t² - 3a*t + 2a² - a - 1 = 0
D = 9a² - 8a² + 4a + 4 = (a+2)² > 0 -- условие для двух корней)))
a ≠ -2
и еще: речь про 2 корня --- для х,
значит, если выражение в первой скобке ( = t ) окажется = 0,
то второй степени для аргумента не станет и о двух корнях речи не будет...
вывод: логарифмы не должны быть равны)))
т.е. x+a ≠ x-a
0 ≠ -2a
a ≠ 0
и еще дополнение))) спасибо внимательному LNT64
в случае равенства свободного члена нулю, уравнение, конечно же, остается квадратным (относительно t ))), но становится неполным квадратным)))
и для (t) решения два, а вот для аргумента (х) -- уже нет)))
т.к. получаются равными логарифмы)))
и из условия 2а² - a - 1 ≠ 0 получим еще
а ≠ (1 +- 3) / 2
а ≠ 1
а ≠ -1/2
теперь уже вроде все)))
не зря сначала решение показалось подозрительно легким)))
Автор ответа:
0
Для a<0, мне надо еще решать.
Автор ответа:
0
Ответ: (-oo; -0,5) U (-0,5; 0) U (1; +oo).
Автор ответа:
0
Ответ: (-oo; -2) U (-2; -0,5) U (-0,5; 0) U (1; +oo). Кажется так.
Автор ответа:
0
очень похоже на наше общее решение)))
Автор ответа:
0
только у Вас больше времени ушло)))
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: laofille
Предмет: Математика,
автор: Аноним