Предмет: Математика,
автор: glagoleva
степени и лагорифмы!!
Приложения:
Ответы
Автор ответа:
0
Ответы:
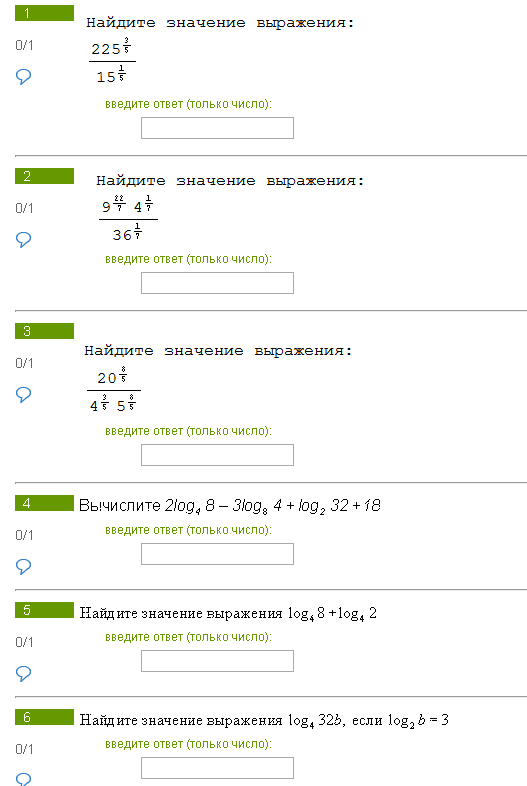
№1: 15
№2: 729
№3: 1 (если там везде степени 8/5. очень плохо видно в знаменателе степень числа 4. Если в знаменателе, там где 4 степень 9/5, то ответ будет 4^ -1/5)
№4: 24
№5: 2
№6: 4
Пояснение задания №1.
Числитель 225^3/5. 225(пока без учета степени) представляем как 15^2. Полученную степень 2 перемножаем со степенью 3/5. Получаем 6/5. По свойству степеней, так как выполняется деление, то степени с одинаковым основанием вычитаются: 15 ^ 6/5 : 15 ^ 1/5 = 15 ^ 5/5 =15.
Пояснение задачи №2:
Знаменатель 36^1/7. Раскладываем это число как 9^1/7 x 4^1/7. Получаем одинаковые основания и в числителе, и в знаменателе. Вычитаем степени и получаем результат.
Пояснение задачи №4.
Тут нужно знать свойства логарифмов.
Самое основной свойство логарифмов, связанное со степенями:
Пример:
И число, и основание в данном случае, нужно сделать так, чтобы и то и другое было равно друг другу, чтобы в результате получить равное единице: . Так 4 можно представить как 2^2, а 8 как 2^3. Привели. Дальше надо усвоить, что степени можно вынести за логарифм, при чем степень числа будет являться числителем коэффициента, а основание - знаменателем. Т.е, в данном примере получится коэффициент 3/2 и пример будет выглядить таким образом: 3/2
. Так 4 можно представить как 2^2, а 8 как 2^3. Привели. Дальше надо усвоить, что степени можно вынести за логарифм, при чем степень числа будет являться числителем коэффициента, а основание - знаменателем. Т.е, в данном примере получится коэффициент 3/2 и пример будет выглядить таким образом: 3/2  .
.
Пояснение задачи №6.
Тут действуют формулы:


В данном случае мы берем формулу 1, где сложение и умножение. Из умножения мы разбиваем каждый логарифм, выполняя сложение. И дальше опять приводим основание и число к одному, вынося степени как коэффициент.
*Прочие формулы:


№1: 15
№2: 729
№3: 1 (если там везде степени 8/5. очень плохо видно в знаменателе степень числа 4. Если в знаменателе, там где 4 степень 9/5, то ответ будет 4^ -1/5)
№4: 24
№5: 2
№6: 4
Пояснение задания №1.
Числитель 225^3/5. 225(пока без учета степени) представляем как 15^2. Полученную степень 2 перемножаем со степенью 3/5. Получаем 6/5. По свойству степеней, так как выполняется деление, то степени с одинаковым основанием вычитаются: 15 ^ 6/5 : 15 ^ 1/5 = 15 ^ 5/5 =15.
Пояснение задачи №2:
Знаменатель 36^1/7. Раскладываем это число как 9^1/7 x 4^1/7. Получаем одинаковые основания и в числителе, и в знаменателе. Вычитаем степени и получаем результат.
Пояснение задачи №4.
Тут нужно знать свойства логарифмов.
Самое основной свойство логарифмов, связанное со степенями:
Пример:
И число, и основание в данном случае, нужно сделать так, чтобы и то и другое было равно друг другу, чтобы в результате получить равное единице:
Пояснение задачи №6.
Тут действуют формулы:
В данном случае мы берем формулу 1, где сложение и умножение. Из умножения мы разбиваем каждый логарифм, выполняя сложение. И дальше опять приводим основание и число к одному, вынося степени как коэффициент.
*Прочие формулы:
Автор ответа:
0
замечательно *0*
Похожие вопросы
Предмет: Английский язык,
автор: azizaabilbasar
Предмет: Английский язык,
автор: rustemsqrov
Предмет: Окружающий мир,
автор: DashaVERTEGEL
Предмет: Биология,
автор: нюк242
Предмет: Математика,
автор: nacstyabryance