Question

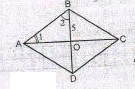
Дан чертеж, угол 1 на 30 градусов меньше угла 2. Найти: AB, Sabcd

Answer 1

Ответ:

50√3 (ед²).

Объяснение:

Рассмотрим ΔАОВ, прямоугольный, т.к. образован диагоналями ромба (диагонали ромба пересекаются под прямым углом).

Сумма острых углов прямоугольного треугольника составляет 90°, отсюда ∠2=90-30=60°;  ∠1=60-30=30°.

Катет, лежащий против угла 30°, равен половине гипотенузы, поэтому АВ=2ВО=5*2=10 (ед. изм.)

Площадь ромба S=½d₁d₂.

Диагонали ромба в точке пересечения делятся пополам, поэтому ВD=2ВО=5*2=10 (ед. изм)

АВ=АD=ВО=10, значит, ΔАВD - равносторонний, АО - высота.

Найдем АО по формуле высоты равностороннего треугольника

АО=АВ√3/2=10√3/2=5√3 (ед. изм.)

АС=2АО=10√3 (ед. изм.)

S(ABCD)=½ * 10√3 * 10 = 50√3 (ед²).

(Решение справедливо в том случае, если ABCD - ромб, чего в условии не сказано).