Предмет: Математика,
автор: Margosha001
Первообразная и интеграл
Помогите пожалуйста с решением примера, как можно быстрее
примеры выделены римской цифрой 1
Приложения:
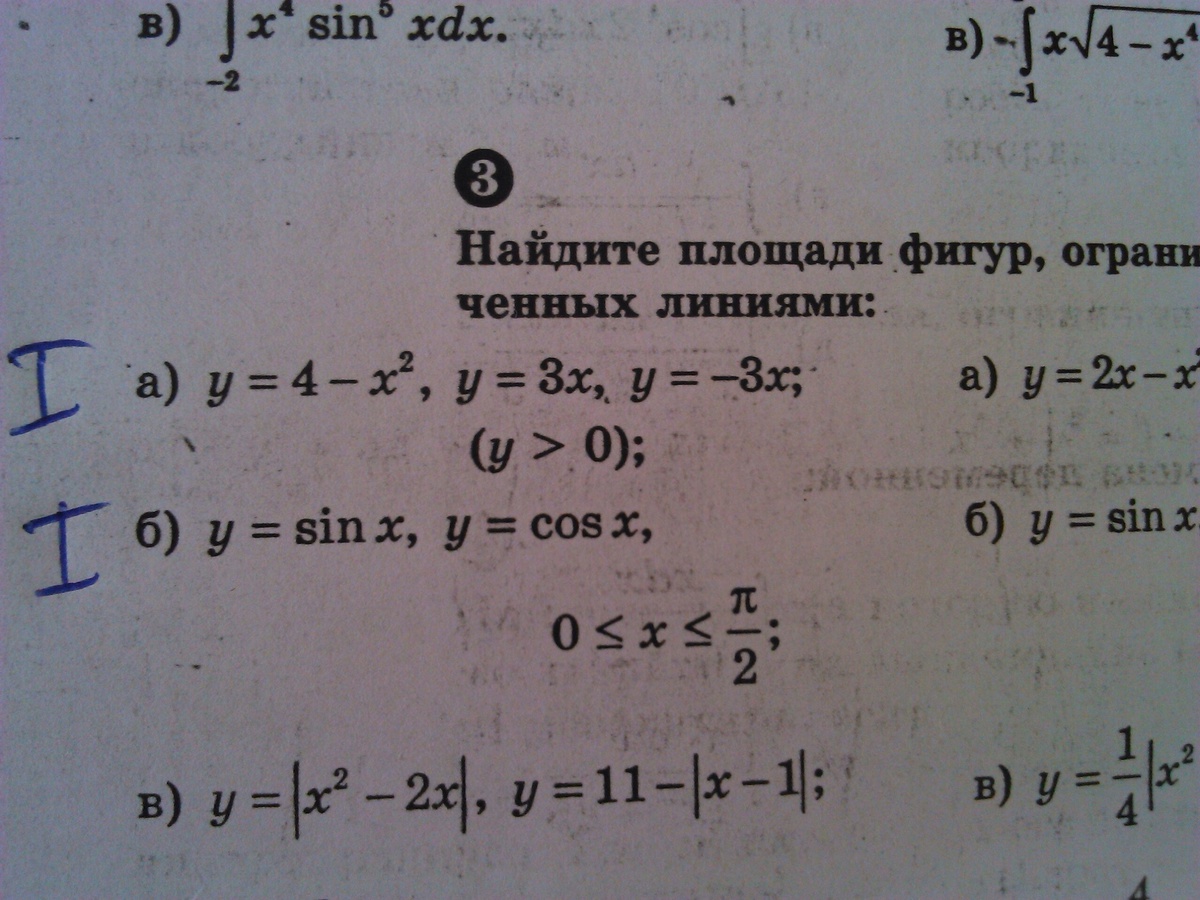
Ответы
Автор ответа:
0
первое: там 3 графика. они симметричны относительно оси Оy. Найдем пересечение этих графиков:
4-x^2 = 3x => x^2 +3x-4 = 0 => x = -4 & 1
Так как нас просят найти площадь сектора при x > 0 значит нам требуется только x = 1
Теперь возьмем интеграл.


3 - 3/2 = 3/2 - площадь сектора, ограниченного графиками функций 4-x^2, 3x и осью Oy. Чтобы найти площадь всего сектора, надо полученную площадь удвоить.
получим S = 3
Во втором примере:
мы знаем что cosx = sinx при


Вычетаяи первого интеграла второй, получим
Но это опять же только левая половина сектора. Нам нужно доможить эту площадь на 2, чтобы получить всю площадь.
S =
4-x^2 = 3x => x^2 +3x-4 = 0 => x = -4 & 1
Так как нас просят найти площадь сектора при x > 0 значит нам требуется только x = 1
Теперь возьмем интеграл.
3 - 3/2 = 3/2 - площадь сектора, ограниченного графиками функций 4-x^2, 3x и осью Oy. Чтобы найти площадь всего сектора, надо полученную площадь удвоить.
получим S = 3
Во втором примере:
мы знаем что cosx = sinx при
Вычетаяи первого интеграла второй, получим
Но это опять же только левая половина сектора. Нам нужно доможить эту площадь на 2, чтобы получить всю площадь.
S =
Похожие вопросы
Предмет: Математика,
автор: din8825
Предмет: Қазақ тiлi,
автор: nazerkekulimova17
Предмет: Литература,
автор: vladislaavva
Предмет: Математика,
автор: chertovka000
Предмет: Математика,
автор: newbrid