Предмет: Геометрия,
автор: noody1
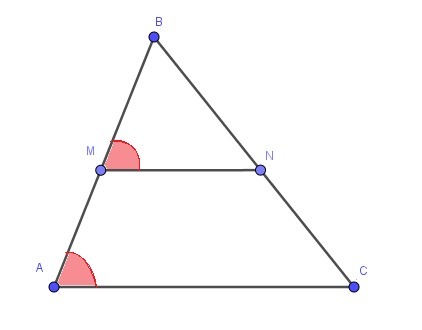
прямая параллельная стороне AC треугольника ABC пересекает стороны AB и BC в точках М и N соответственно. найдите BN если МС=18, АС=42, NC=40
Ответы
Автор ответа:
0
Здесь скорее всего опечатка в условие. Полное условие предоставляется.
Задача. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 18, AC = 42, NC = 40.
Решение:
У треугольников MBN и ABC угол В - общий и ∠BMN = ∠BAC как соответственные углы, следовательно, треугольники MBN и ABC подобны по двум углам.
Ответ: 30.
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: niyazovasafiya200743
Предмет: Математика,
автор: ktrutkovaelena780
Предмет: Математика,
автор: alino4ka200e2
Предмет: Алгебра,
автор: skaip9nik