Question

В треугольнике ABC точка N лежит на стороне AC, AN=2/5AC, медиана AM перпендикулярна BN. Найти площадь треугольника ABC, если AM=m, BN=n.
Объясните решение, пожалуйста.

Answer 1

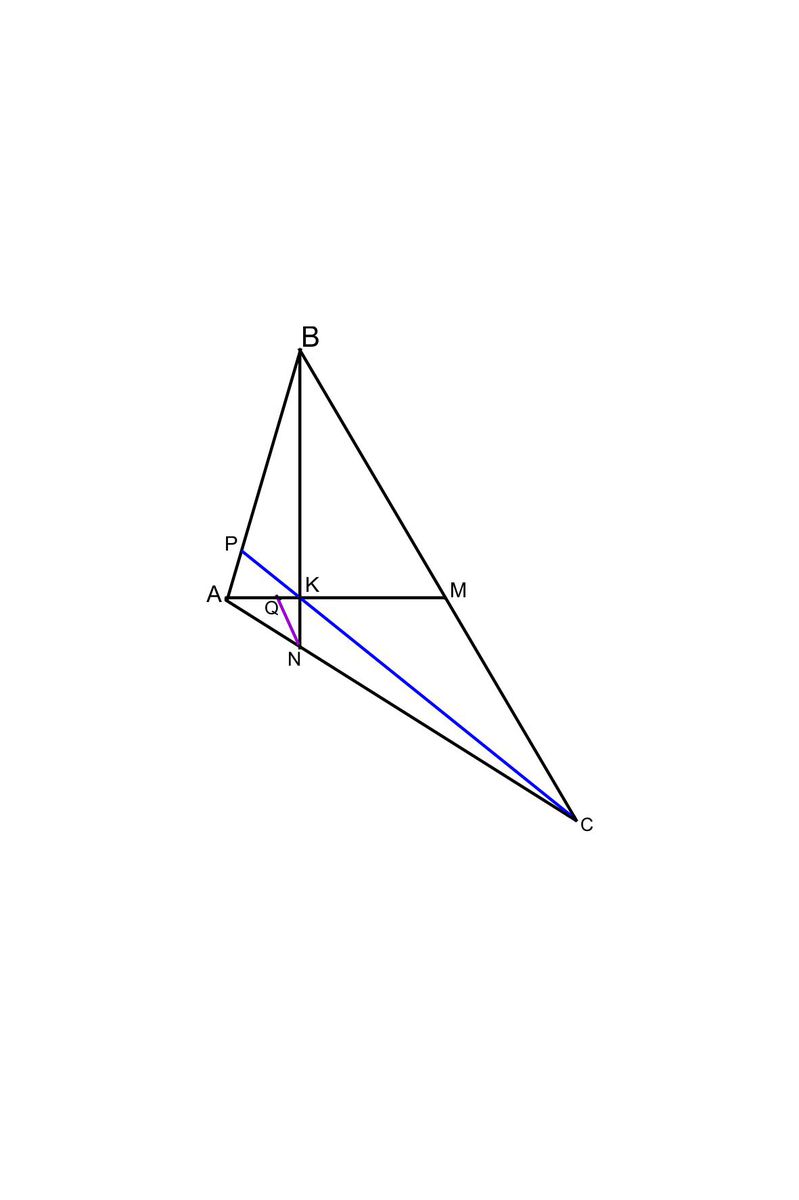
Пусть K - точка пересечения AM и BN. Для решения задачи достаточно найти BK.
1) Если предположить, что автор знаком с теоремой Чевы, а так же - с теоремой Ван-Обеля, то 
если продолжить CK до пересечения с AB в точке P, то AP/PB = AN/NC = 2/3; поскольку BM - медиана, BM/MC = 1;
то есть BP/PA = 3/2;
Отсюда BK/KN = 3/2 + 1 = 5/2; то есть BK = n*5/7; 
2) В том случае, если теорема Чевы неизвестна, задача тоже легко решается.
Если провести NQ II CB; точка Q лежит на AM, то из подобия треугольников ANQ и ACM следует NQ/CM = 2/5; 
треугольники QKN и MKB тоже подобны, и MB = CM; отсюда NK/BK = NQ/MB = 2/5;
то есть BK = n*5/7; ( а NK = n*2/7, само собой)

Ясно, что площадь ABC равна удвоенной площади AMB, то есть равна
S = BK*AM = m*n*5/7;

Answer 2

Видимо я 9 класс уже забыл...

Answer 3

Могу и подсказать - проще доказать "почти обратное" утверждение - провести через B' прямую B'C' II BC, соединить K с С и C' и из всякого подобия возникших там тр-ков доказать, что CK и C'K "сливаются" в одну линию.

Answer 4

Я уже разобрали по теореме Менелая

Answer 5

ну дело ваше