Предмет: Математика,
автор: AnnaLik
помогите!!!! Найдите точку максимума фукнции
Приложения:
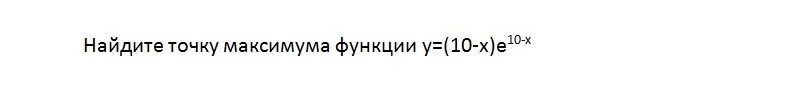
Ответы
Автор ответа:
0
Теперь найдем точку пересечения производной с осями координат.
Так как
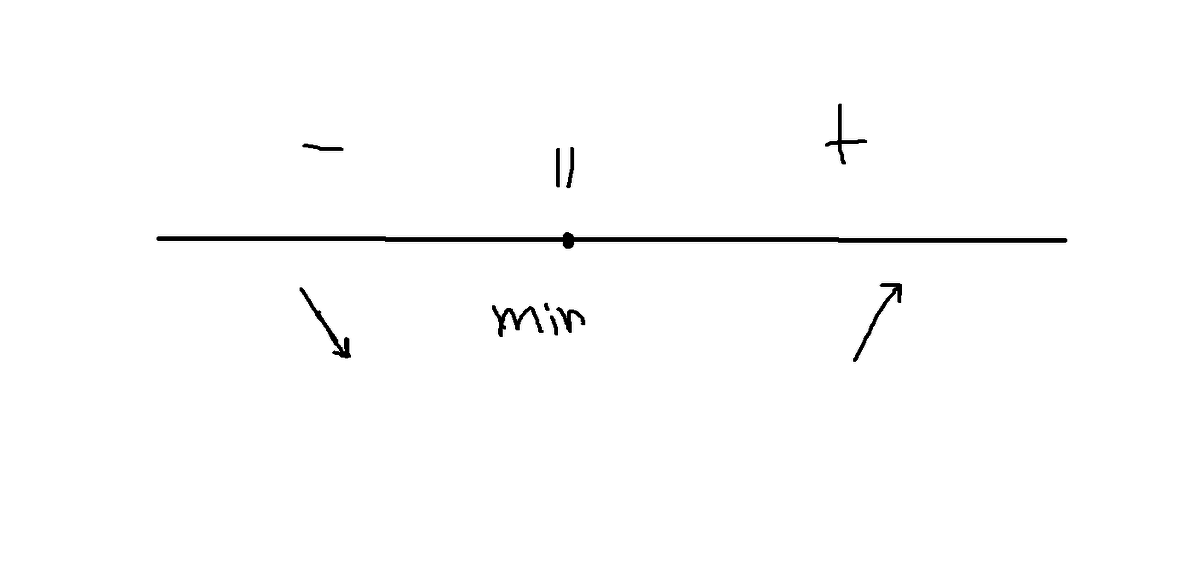
Далее см.рисунок.
Итог: У этой функции нет точки максимума. Но есть точка минимума: x=11.
Приложения:

Автор ответа:
0
а можно поподробнее всё расписать?
Автор ответа:
0
да, спасибо)
Автор ответа:
0
Приложения:


Похожие вопросы
Предмет: Математика,
автор: dzakupovdalvar
Предмет: Биология,
автор: sfjfhuhu
Предмет: Музыка,
автор: lagovskaaksenia3
Предмет: Математика,
автор: маринанина