Предмет: Геометрия,
автор: elfiruza
В правильной четырехугольной пирамиде SABCD , в которой АВ=2,SA=3 точка Е - середина SB. Найдите угол между прямой СЕ и плоскостью SBD?
Ответы
Автор ответа:
0
a=АВ=BC=DC=AB=2 (стороны квадрата ABCD )
r = SA = SB = SD = SC=3 (ребра пирамиды)
d - диагонали квадрата основания пирамиды
h- высота пирамиды
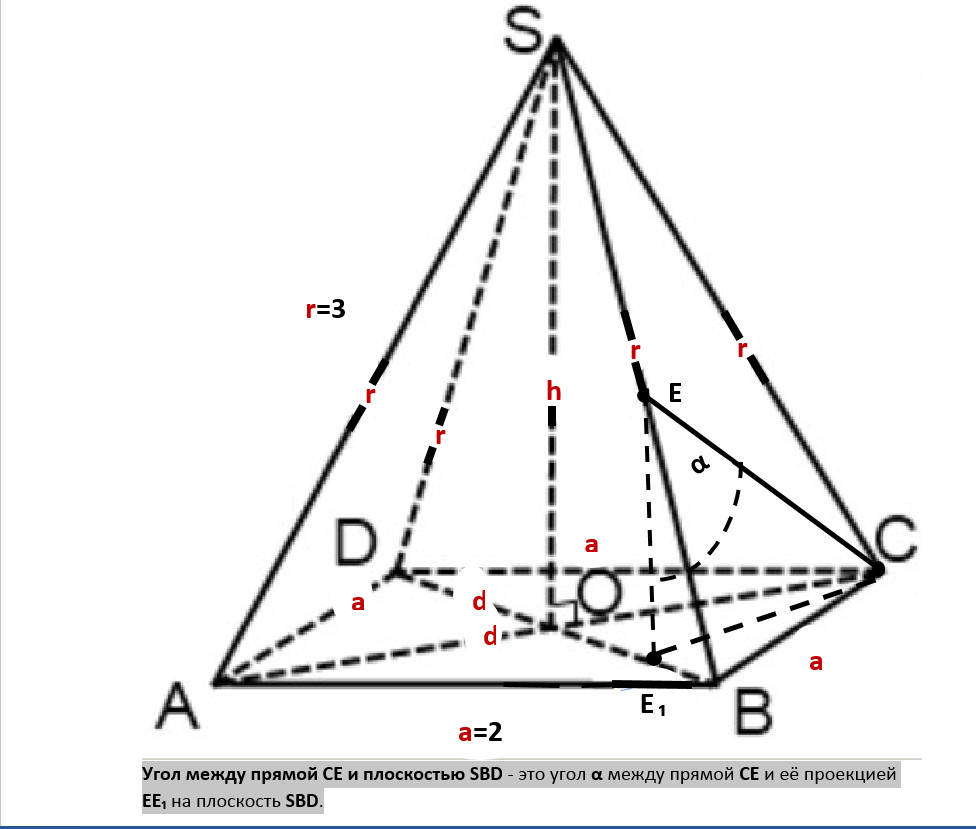
Угол между прямой СЕ и плоскостью SBD - это угол α между прямой СЕ и её проекцией EE₁ на плоскость SBD.
tgα=CE₁/EE₁
EE₁=h/2
h²=r²-(d/2)²
d²=a²+a²=2a²
d=a√2=2√2
h²=r²-(d/2)²=3²-(2√2/2)²=3²-2=9-2=7
h=√7
EE₁=h/2=(√7)/2
EE₁=(√7)/2
CE₁²=a²-BE₁²
BE₁=d/4
d=a√2
BE₁=d/4=(a√2)/4
CE₁²=a²-BE₁²
CE₁²=a²-BE₁²=a²-((a√2)/4)²
CE₁²=a²(1-2/16)=a²(14/16)=7*a²/8=7*2²/8=7/2
CE₁²=7/2
CE₁=√(7/2)
tgα=CE₁/EE₁=(√7/√2):(√7)/2=2/√2=√2
tgα=√2
α=arctg(√2) ≈ 55°
рисунок ниже:
r = SA = SB = SD = SC=3 (ребра пирамиды)
d - диагонали квадрата основания пирамиды
h- высота пирамиды
Угол между прямой СЕ и плоскостью SBD - это угол α между прямой СЕ и её проекцией EE₁ на плоскость SBD.
tgα=CE₁/EE₁
EE₁=h/2
h²=r²-(d/2)²
d²=a²+a²=2a²
d=a√2=2√2
h²=r²-(d/2)²=3²-(2√2/2)²=3²-2=9-2=7
h=√7
EE₁=h/2=(√7)/2
EE₁=(√7)/2
CE₁²=a²-BE₁²
BE₁=d/4
d=a√2
BE₁=d/4=(a√2)/4
CE₁²=a²-BE₁²
CE₁²=a²-BE₁²=a²-((a√2)/4)²
CE₁²=a²(1-2/16)=a²(14/16)=7*a²/8=7*2²/8=7/2
CE₁²=7/2
CE₁=√(7/2)
tgα=CE₁/EE₁=(√7/√2):(√7)/2=2/√2=√2
tgα=√2
α=arctg(√2) ≈ 55°
рисунок ниже:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: lkurcanidi
Предмет: Другие предметы,
автор: sarsenbajajsolpan
Предмет: Английский язык,
автор: oj1
Предмет: География,
автор: showy27