Question

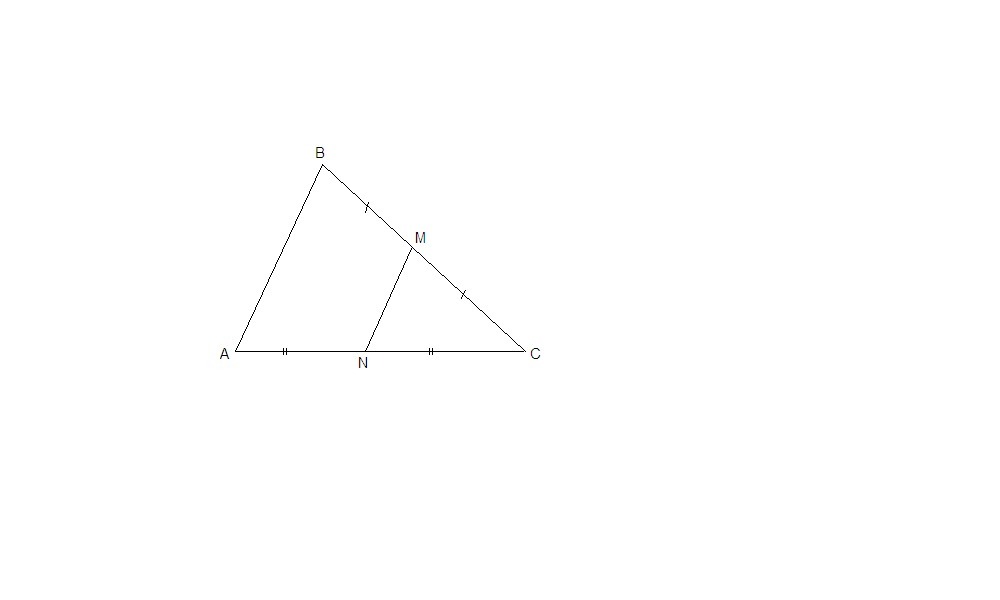
В треугольнике АВС отмечены середины M и N сторон ВС и АС соответственно .Порщадь CNM равна 67.Найдите площадь четырехугольника ABMN

Answer 1

MN║АВ как средняя линия ΔАВС.
∠CMN = ∠CВА как соответственные при пересечении параллельных прямых MN  и АВ секущей СВ,
∠АСВ - общий для треугольников АВС и NMC, ⇒
ΔАВС подобен  ΔNMC по двум углам.
Коэффициент подобия:
k = AB : MN = 2 : 1
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Sabc : Snmc = 4 : 1
Sabc : 67 = 4 : 1
Sabc = 67 · 4 = 268
Sabmn = Sabc - Snmc = 268 - 67 = 201