Question

 

На отрезке AB выбрана точка C  так ,что 
AC=21 и BC=8. Построена окружность с
центром  A ,проходящая
через C .Найдите длину
отрезка касательной, проведённой из точки B  к этой окружности.  

Answer 1

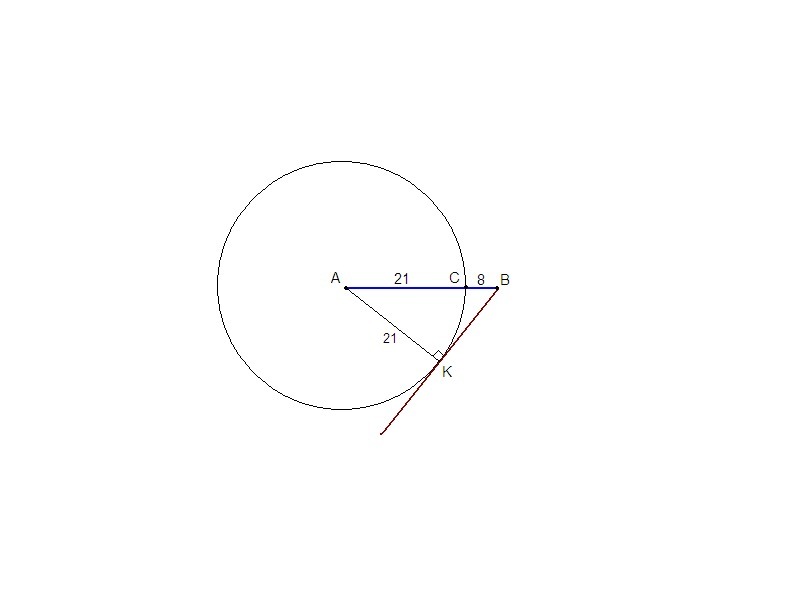
Проведем касательную ВК к окружности (К - точка касания).

АК⊥ВК как радиус, проведенный в точку касания.

АК = АС = 21 как радиусы.

Из прямоугольного треугольника АВК по теореме Пифагора:

ВК = √(АВ² - АК²) = √(29²- 21²) = √((29 - 21)(29 + 21)) = √(8 · 50) = √400 = 20