Предмет: Геометрия,
автор: misssamandrako
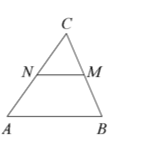
В треугольнике ABC отмечены середины M и N сторон BC и AC. Площадь треугольника CNM равна 2. Найдите площадь четырёх угольника ABMN.
Приложения:
Ответы
Автор ответа:
0
Так как АN=NC, CM=BM⇒MN-средняя линия ΔАВС
ΔАВС подобен ΔCNM по трем углам⇒ площадь АВС/площадь CNM=4/1(коэффициент подобия равен 2(CN/AC=1/2), а площади подобных фигур относятся как коэффициент подобия в квадрате)
Площадь АВС=2*4=8
Площадь АВMN=8-2=6
Ответ: 6.
ΔАВС подобен ΔCNM по трем углам⇒ площадь АВС/площадь CNM=4/1(коэффициент подобия равен 2(CN/AC=1/2), а площади подобных фигур относятся как коэффициент подобия в квадрате)
Площадь АВС=2*4=8
Площадь АВMN=8-2=6
Ответ: 6.
Похожие вопросы
Предмет: История,
автор: agniyazd
Предмет: Алгебра,
автор: TheFillarMoon
Предмет: Русский язык,
автор: nmatvey112meld
Предмет: Алгебра,
автор: ZzzzKmmm