Предмет: Алгебра,
автор: аниковигор18
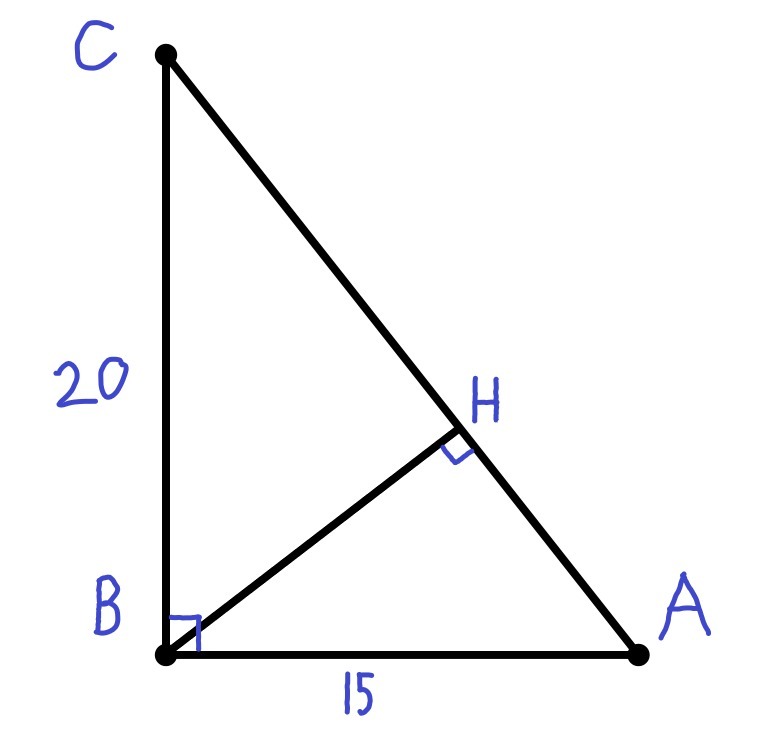
катеты прямоугольного треугольника равны 15 и 20 найдите высоту проведенную к гипотенузе
Ответы
Автор ответа:
0
Пусть катеты прямоугольного треугольника равны a и b, а его гипотенуза - c; h - высота.
Найдем гипотенузу c, используя теорему Пифагора
Площадь прямоугольного треугольника равна кв.ед., а с другой стороны, площадь треугольника равна
кв.ед.
Приравнивая площади , будем иметь уравнение:
Ответ: 12.
Автор ответа:
0
Найдём AC по теореме пифагора
Площадь треугольника ABC равна половине произведения катетов
Воспользуемся ещё одной формулой площади треугольника, чтобы найти BH
Ответ: 12
Приложения:
Похожие вопросы
Предмет: Математика,
автор: haybitch
Предмет: Алгебра,
автор: instadiava
Предмет: Алгебра,
автор: polinaboginia
Предмет: Биология,
автор: 123b
Предмет: Математика,
автор: anton3124