Question

Помогите пожалуйста пару задач решить
Какие из следующих утверждений верны?
1)Tреугольника со сторонами 1,2,4 не существует
2)Две прямые перпендикулярные третьей прямой ,перпендикулярны друг другу.
3)У любой трапеции основания параллельны.


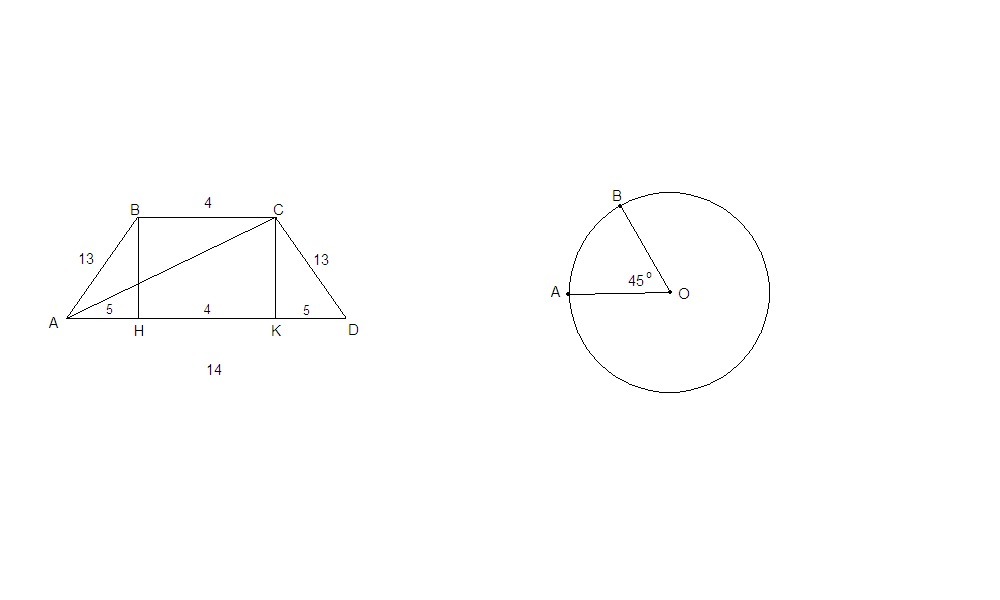
Основания равнобедренной трапеции равны 4 и 14 ,боковая сторона равна 13.Найдите длину диагонали трапеции.


И последняя.

На окружности с центром точки О отмечены точки А и B так, что угол АОB=45градусов 
.Длина меньшей дуги AB равна 91 .Найдите длину большей дуги

Answer 1

1.
Верны 1 и 3 утверждение.

2. Проведем высоты трапеции ВН и СК. ВСКН - прямоугольник, значит
НК = ВС = 4
ΔАВН = ΔDCK по гипотенузе и катету (АВ = CD так как трапеция равнобедренная, ВН = СК как высоты), ⇒
АН = DK = (AD - HK)/2 = (14 - 4)/2 = 5
АК = АН + НК = 5 + 4 = 9
ΔCKD:  по теореме Пифагора
             СК = √(CD² - KD²) = √(169 - 25) = √144 = 12
ΔАСК: по теореме Пифагора
           АС = √(АК² + СК²) = √(81 + 144) = √225 = 15

3.
Угол, соответствующий большей дуге АВ:
360° - 45° = 315°
315° / 45° = 7 - он в 7 раз больше угла, соответствующего меньшей дуге.
Значит и длина большей дуги в 7 раз больше:
91 · 7 = 637