Предмет: Геометрия,
автор: lednewazlata
в треугольнике ABC AB=BC=75, AC=120
Найти длину медианы BM.
Ответы
Автор ответа:
0
Медиана делит сторону пополам поэтому АМ=АС/2=120/2=60
За т. Пифагора ВМ=√АВ²-АМ²=√5625-3600=√2025=45
За т. Пифагора ВМ=√АВ²-АМ²=√5625-3600=√2025=45
Автор ответа:
0
благодарю
Автор ответа:
0
так как треугольник равнобедренный (по условию), медиана BM не только делит противоположную сторону пополам, но и является высотой ( идет под прямым углом)
тогда мы получаем прямоугольный треугольник AMB. Рассмотрим его.
Катет AM = 120/2 = 60
а дальше по теореме пифагора
мы знаем гипотинузу и катет, следовательно BM = 60^2 + BM^2 = 75^2
3600 + BM^2 = 5625
BM^2 = 5625 - 3600 = 2025
BM = 45
тогда мы получаем прямоугольный треугольник AMB. Рассмотрим его.
Катет AM = 120/2 = 60
а дальше по теореме пифагора
мы знаем гипотинузу и катет, следовательно BM = 60^2 + BM^2 = 75^2
3600 + BM^2 = 5625
BM^2 = 5625 - 3600 = 2025
BM = 45
Приложения:
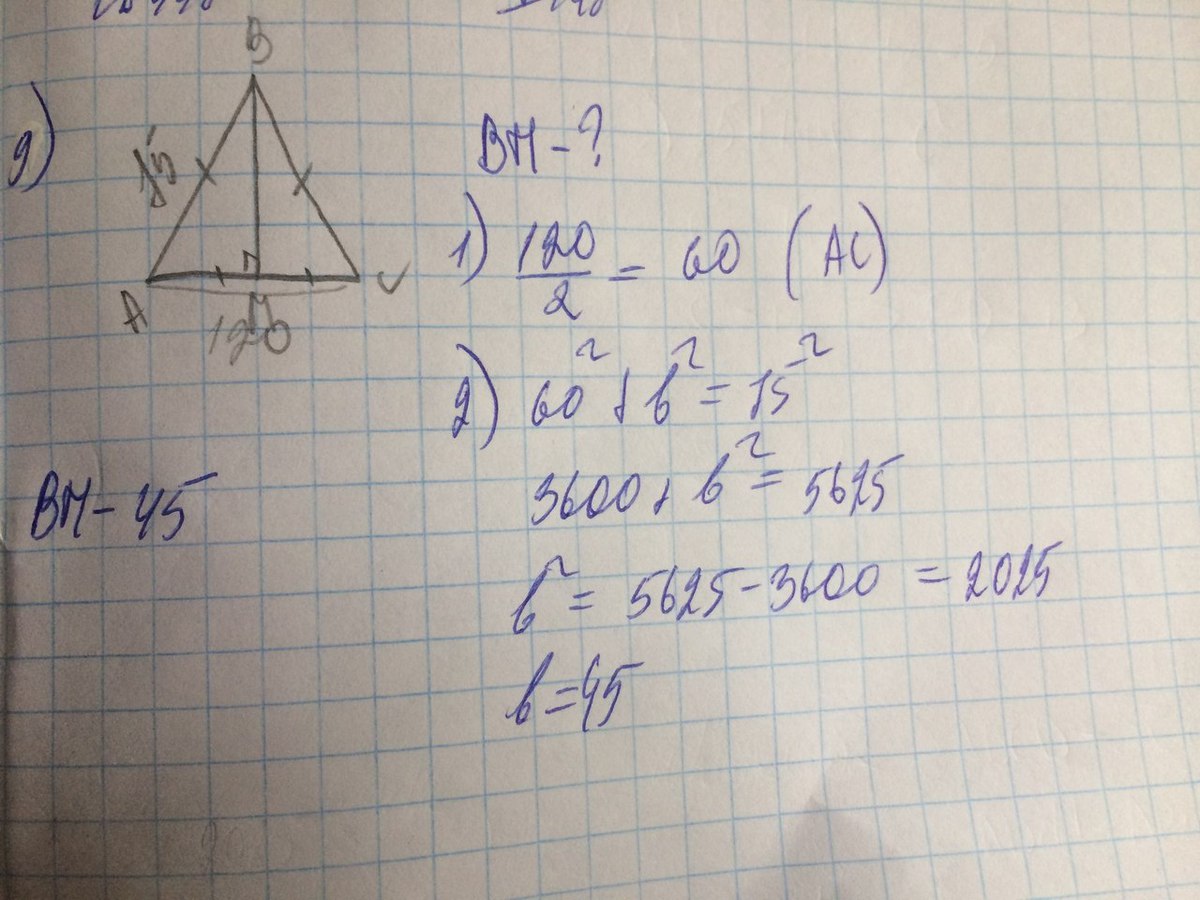
Похожие вопросы
Предмет: Физика,
автор: anastasiasemcenkova3
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: nikitakruc89
Предмет: История,
автор: supun4o